I perfectly understand the definition of a limit which states that:
Given $$ ε > 0 $$, there is some $$δ(ε) > 0 $$ such that $$0 < |x − a| < δ ⇒ |f(x) − b| < ε$$
but why don't we care about when x=a?
Asked
Active
Viewed 203 times
0
-
2Because we want to be able to take limits of functions that are not even defined at $a$, for example $(\sin x)/x$ at $x=0$. – Dec 08 '19 at 03:59
-
Related: https://math.stackexchange.com/questions/1019388/why-are-punctured-neighborhoods-in-the-definition-of-the-limit-of-a-function, https://math.stackexchange.com/questions/1979605/whats-the-purpose-of-the-two-different-definitions-used-for-limit – Hans Lundmark Dec 08 '19 at 07:53
1 Answers
0
Given a function $f\colon \mathbb R\to\mathbb R$ and a real number $x\in\mathbb R$, we can consider the value of the function at $x$, we can consider the left hand limit of the function as we approach $x$ from below, and we can consider the right hand limit as we approach from above.
For a continuous function, all these three numbers (exist and) are equal. But in general, they can all be different, here is an explicit example: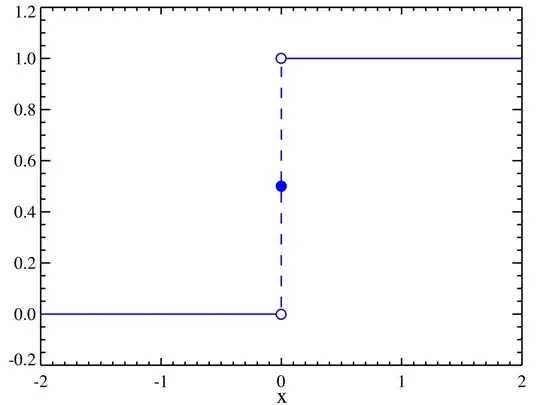
This is a picture of a discontinuous step function. The left hand limit at $x=0$, also denoted $f(0^-)$, is equal to $0$. The value at $0$, denoted $f(0)$, is equal to $\tfrac12$. And the right hand limit, denoted $f(0^+)$, is equal to $1$.
In your definition, the "limit" is actually describing the values of the left and right hand limits, if they are equal - and the limit does not exist, if they are not.
pre-kidney
- 30,223
-
so you are saying that if x=a we will be then talking about continuity am I right? – Yassire Dec 08 '19 at 04:04
-
@Yassire That's correct. One definition of being continuous at a point $c$ is $\lim_{x \to c} f(x) = f(c)$. – Andrew Tawfeek Dec 08 '19 at 04:07
-
Yes, that is correct: if we want to ask whether $f(a)$ is equal to the limit as $|x-a|\to 0$ of $f(x)$, then that is the same as asking whether the function is continuous at $x=a$. – pre-kidney Dec 08 '19 at 04:07