In triangle ABC, find the value of $\sum a^2(\cos^2 B-\cos^2 C)$

Question

The expression is $$a^2(\cos^2 B-\cos^2 C)+b^2(\cos^2 C-\cos^2 A)+c^2(\cos^2 A-\cos^2B)$$ $$=a^2\sin A\sin (C-B)+b^2\sin B \sin (A-C) + c^2\sin C \sin (B-A)$$ $$=k\sin^3A\sin (C-B)+k\sin^3B\sin (A-C) + k\sin ^3 C\sin (B-A)$$ I couldn’t solve further, the answer is an integer value. Thanks!

score 1 · Answer 1 · answered Dec 08 '19 at 01:35

For $\triangle ABC$ we have a rule known as projection rule which states that

$a=b\ cosC+c\ cosB$

$b=c\ cosA+a\ cosC$

$c=b\ cosA+a\ cosB$

The given expression can be re-arranged to be written as

$a^2\cos^2B-b^2\cosÂ+b^2\cos^2C-c^2\cos^2B+c^2\cos^2A-a^2\cos^2C$

$=(a\cos B+b\cos A)(a\cos B-b\cos A)+(b\cos C+c\cos B)(b\cos C-c\cos B)+(c\cos A+a\cos C)(c\cos A-a\cos C)$

$=c(a\cos B-b\cos A)+a(b\cos C-c\cos B)+b(c\cos A-a\cos C)$

$=0$

score 0 · Answer 2 · answered Dec 07 '19 at 16:27

0

Hint:

$$\cos^2B-\cos^2C=1-\sin^2B-(1-\sin^2C)=?$$

Now replace $a$ with $2R\sin A$

answered Dec 07 '19 at 16:27

lab bhattacharjee

274,582

@user600016, I have suggested $$a^2(\cos^2B-\cos^2C)=\cdots=4R^2(\sin^2C\sin^2A-\sin^2A\sin^2B)$$ – lab bhattacharjee Dec 07 '19 at 16:34
Oh sorry my bad – user600016 Dec 07 '19 at 16:42
Isn’t that essentially what I did, unless you don’t mean to use the sin(A-B)sin(A+B) formula – Aditya Dec 07 '19 at 16:45
@Aditya, Have you noticed the cyclic form I've arrived at. You will be entangled if you use https://math.stackexchange.com/questions/175143/prove-sinab-sina-b-sin2a-sin2b – lab bhattacharjee Dec 07 '19 at 18:06
@Aditya, if we write $\sin^2A=p$ etc, we shall get $$4R^2(pq-qr+qr-rp+rp-pq)=?$$ – lab bhattacharjee Dec 07 '19 at 18:14

score 0 · Answer 3 · answered Dec 07 '19 at 16:56

0

Using \begin{align} \cos A&=\frac{-a^2+b^2+c^2}{2bc} ,\\ \cos B&=\frac{a^2-b^2+c^2}{2ac} ,\\ \cos C&=\frac{a^2+b^2-c^2}{2ab} , \end{align}

\begin{align} a^2(\cos^2 B-\cos^2 C)+b^2(\cos^2 C-\cos^2 A)+c^2(\cos^2 A-\cos^2B) &=0 . \end{align}

answered Dec 07 '19 at 16:56

g.kov

13,581

Did you square cosA? Seems a bit too long, no? – Aditya Dec 07 '19 at 16:58
@Aditya: The result would not be zero otherwise. – g.kov Dec 07 '19 at 17:59
I don't think squaring would be expected. There is bound to be a shorter version – Aditya Dec 07 '19 at 18:08

Quanto · Accepted Answer · 2019-12-07T20:58:02.240

Note,

$$I = a^2(\cos^2 B-\cos^2 C)+b^2(\cos^2 C-\cos^2 A)+c^2(\cos^2 A-\cos^2B)$$

$$=4R^2 \left[ \sin^2 A (\cos^2 B-\cos^2 C)+\sin^2 B (\cos^2 C-\cos^2 A)+\sin^2 C (\cos^2 A-\cos^2B)\right]$$

where $R$ is the circumradius. Then, use the identities $\cos^2x = \frac12(1+\cos2x)$ and $\sin^2x= \frac12(1-\cos2x)$ to reexpress $I$ as,

$$\frac I{R^2} = (1-\cos2A)(\cos2B-\cos2C)+ (1-\cos2B)(\cos2C-\cos2A)+ (1-\cos2C)(\cos2A-\cos2B)=0$$

Edit:

$$I = a^2(\sin^2 C-\sin^2 B)+b^2(\sin^2 A-\sin^2 C)+c^2(\sin^2 B-\sin^2A)= \frac{ a^2(c^2-b^2)+b^2(a^2-c^2)+c^2(b^2-a^2)}{4R^2}=0$$

g.kov · Answer 5 · 2019-12-08T01:07:07.767

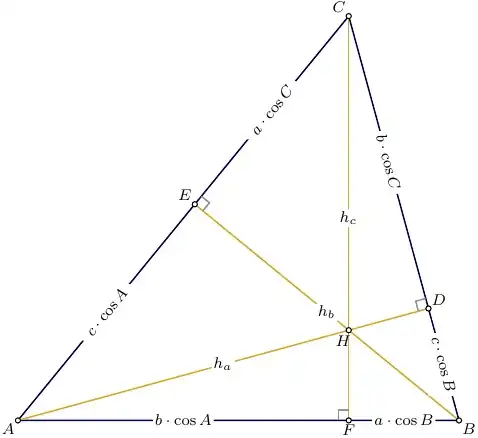
Let $h_a,h_b,h_c$ be the altitudes in corresponding $\triangle ABC$. Consider \begin{align} u&=a^2-h_b^2+b^2-h_c^2+c^2-h_a^2 \\ &= a^2\cos^2 C+b^2\cos^2 A+c^2\cos^2 B ,\\ v&=a^2-h_c^2+b^2-h_a^2+c^2-h_b^2 \\ &= a^2\cos^2 B+b^2\cos^2 C+c^2\cos^2 A \end{align}

\begin{align} 0&=v-u = a^2(\cos^2 B-\cos^2 C)+b^2(\cos^2 C-\cos^2 A)+c^2(\cos^2 A-\cos^2B) . \end{align}

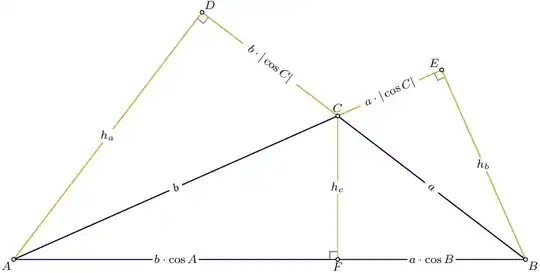
This also holds for obtuse triangles:

In triangle ABC, find the value of $\sum a^2(\cos^2 B-\cos^2 C)$

5 Answers5