For the closed triangular curve prove that $\left|\int_\gamma(e^z+\bar z)dz \right|\le60$

Question

If the $\gamma$ is the closed triangular curve that traces out in counterclockwise fashion the square of vertices $0,3i,-4$ prove that $$\left|\int_\gamma(e^z+\bar z)dz \right|\le60$$

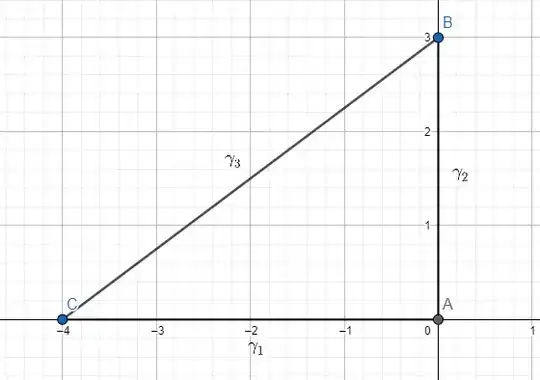
Attempt 1:

Direct calculation with triangle inequality: On $\gamma_1$: $y=0$, $x\in[-4,0]$ so $|e^z+\bar z|=|e^x+x|\le |e^x|+|x|$

Calculating integrals seperately:

$\int\limits_{-4}^0 e^x dx$ and $\int\limits_{-4}^0 x dx$

and for the other paths, I have found a bigger value than $60$

Attempt 2:

I tried to use $\max{|e^z+\bar z|}$ on a given path $\gamma_i$ as : $\max{|e^x|+|x|}$ on $\gamma_1$ is $e^0+|-4|=5$ but for other paths again I have found a bigger value than $60$

How to do it properly?

Answer 1

Re “Attempt 2”: $$ |e^z+\bar z| \le |e^z| + |z| = e^{\operatorname{Re}(z)} + |z| \le e^0 + 4 = 5 $$ holds everywhere on the path $\gamma$, which has the length $12$, so that $$ \left|\int_\gamma(e^z+\bar z)dz \right| \le \int_\gamma |e^z + \bar z| \, |dz| \le 5 \cdot 12 = 60 \, . $$

As mentioned in the comments, this bound can be improved if you know that $\int_\gamma e^z \, dz = 0$.

Remark: The integral can be computed exactly because $\int_\gamma e^z \, dz = 0$ and $$ \int_\gamma \bar z \, dz = 2i A = 12i $$ where $A$ is the oriented area enclosed by $\gamma$, see for example What is the value of $\int_{\gamma} \bar{z} dz$?.