0

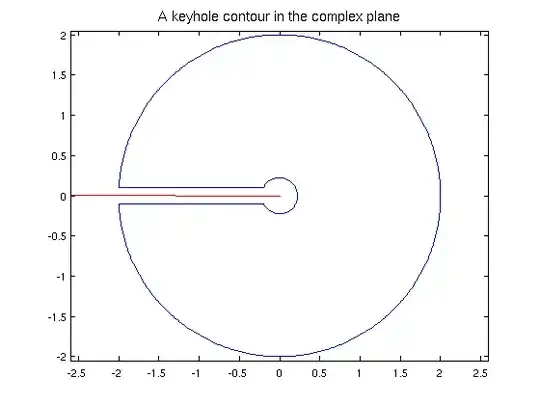
Assume that the only singularities of a function h(z) are finitely many poles that lie away from the origin and the negative real axis. Show that integration of the function f(z) = h(z)ln z, with − π < arg(z) ≤ π, around an appropriate keyhole contour, leads to being able to find the value of the integral of h(-x)dx between 0 and infinity.

I have some idea with how to go about this question, by sketching an appropriate keyhole contour and considering each case separately, but I am unsure on how to start and what to consider for the contour. Thanks.

S.k
  • 1

1 Answers1

0

The whole reason we need to consider a keyhole contour in this case is that the behavior of $\log(z)$ is complicated near $0$ and the negative axis (i.e., it's a branch cut, rather than a pole).

Therefore, trying a contour that looks like this (image obtained here) might be a good idea. enter image description here

Remember that this contour is to deal with the $\log(z)$ part. To deal with the poles of $h(z)$, you may need to cut out more poles from this contour. The key idea is to obtain an estimate of the integral on (boundary of this contour)-(the boundary that you need for the integral), and use Residue Theorem.

Yuxin Wang
  • 575
  • Thanks that's very helpful. May I ask, what do you mean by cutting more poles from the contour? – S.k Dec 04 '19 at 22:01
  • @S.k The other poles can be treated in the same manner as general meromorphic functions. For instance, look at https://math.stackexchange.com/questions/621131/real-integral-by-keyhole-contour – Yuxin Wang Dec 05 '19 at 20:21