0

I am given two points and an unknown third number. I wish to find the equation $(a,b,c)$ for a parabola. I tried solving a system of equations using $x=y^2+y+$ and the two points, as well as treating the third number as the slope of the tangent line to one of the points. This yielded the correct values for the two given points, but very large negative numbers for everything in between. Anyone have an intuition to how I may find the expected parabola?

My inputs are roughly: $P_1 = [1260,1742]$ $P_2 = [1742,1256]$ unknown $= -120$

And the expected parabola looks like this: enter image description here

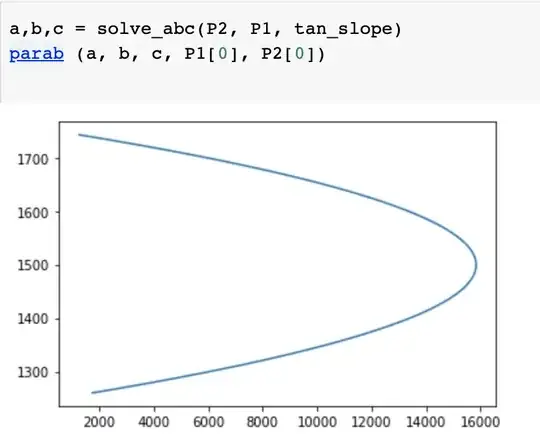
If I choose -120 as the slope for the last point I get the below result: enter image description here

The resulting a,b,c is: $(-0.2461819548547251, 738.2089260678524, -537562.1223900858)$

PandaBearSoup
  • 101
  • Is it $x=ay^2+by+c$ or $y=ax^2+bx+c$? Otherwise, is the picture you have above part of a parabola opening down or to the left? – Andrei Dec 02 '19 at 18:24
  • it's hard to tell without knowing the meaning of the "unknown" number.Three points are necessary to define a unique parabola. – Vasili Dec 02 '19 at 18:25
  • @Andrei I'm not sure but I assumed it was opening to the left so I wrote in that form. – PandaBearSoup Dec 02 '19 at 18:26
  • Did you choose -120 the slope at the first point or at the last? The slope from $P_1$ to $P_2$ is about $-1$. So a slope of $-120$ is almost vertical. – Andrei Dec 02 '19 at 18:34
  • @Andrei I edited my question to include the plotted line if I use -120 as the slope for the last point. This uses the left/right form of the equation to plot. – PandaBearSoup Dec 02 '19 at 18:43
  • I can see from the latest picture that your slope at the last point is positive – Andrei Dec 02 '19 at 18:45
  • Please input your calculations for a, b, c. – Andrei Dec 02 '19 at 18:50
  • @Andrei sorry for the confusion, the system of equations I solved for I used the form y = ax... and then when I plot I swap x and y. The slope is negative if I plot x,y normally. – PandaBearSoup Dec 02 '19 at 18:51
  • When you swap x and y, the slope is $-1/(-120)$ – Andrei Dec 02 '19 at 21:38
  • Just an observation: In projective geometry you can think of this as defining a conic sections by three points and two tangents. Two of the points and one of the taverns are part of your description. The line at infinity as a tangent makes the conic a parabola, and $[1:0:0]$ as the homogeneous coordinates of a point at infinity fix the $x$ direction as the asymptotic direction. Having two defining points sit on the tangent lines reduces the number of solutions from 4 to 1. I might have elegant formulas for this somewhere, need to search... – MvG Dec 02 '19 at 22:53

0 Answers0