Does there exist something like $\frac{dy}{dx^2}$? Does taking higher "w.r t"s lead to trivial results? If no, when do we differentiate w.r.t $x^2$ or higher power. And what is the procedure to take derivative of a function w.r.t say, $x^2$?
-
1Using the chain rule we have that $$\frac{\mathrm{d}y}{\mathrm{d}(x^2)}=\frac1{2x}\cdot\frac{\mathrm{d}y}{\mathrm{d}x}$$ – Peter Foreman Dec 01 '19 at 14:44
-
@PeterForeman and how is that? – Rew Dec 01 '19 at 14:54
2 Answers
You can think that $y$ is a function of some variable, say $\alpha$, which is in turn a function of $x$. In your case, it is $\alpha \left( x \right) = x^2$. Then, effectively $y$ is a function of $x$. If both $y$ and $\alpha$ are differentiable in terms of their variables, then $y$ is differentiable with respect to $x$, i.e., $\dfrac{dy}{dx}$ exist.
Now, the chain rule suggests that
$$\dfrac{d}{dx} y \left( \alpha \left( x \right) \right) = \dfrac{dy}{d\alpha} \dfrac{d \alpha}{dx}.$$
In your case, it would become
$$\dfrac{dy}{dx^2} = \dfrac{dy}{dx} \left( \dfrac{1}{\frac{dx^2}{dx}} \right) = \dfrac{1}{2x} \dfrac{dy}{dx},$$
as mentioned in one of the comments.
- 3,997
- 1
- 13
- 33
Explanation 1: Variables
Recall that the derivative, $\frac{\mathrm{d}y}{\mathrm{d}x}$, represents the change in an dependent variable $y$, corresponding to a change in its independent variable $x$, when that change is very small *. Equivalently, $\frac{\mathrm{d}y}{\mathrm{d}\color{red}{u}}$ represents the change in $y$ corresponding to a small change in another variable, $u$. This is also true when $u$ is dependent on $x$.
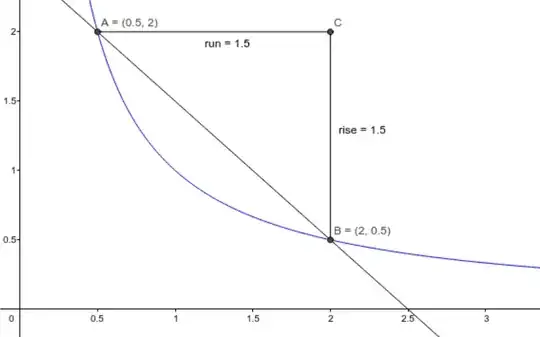
Geometrically, we can envision this with the graph of a curve on an $xy$-plane, as in the picture below. When we pick two points on the curve, this will correspond to a pair of values: the horizontal change (run, $\mathrm{d}x$) and vertical change (rise, $\mathrm{d}y$), whose ratio, $\frac{\mathrm{d}y}{\mathrm{d}x}$, is the slope or derivative. Intuitively, you can think that dividing both sides of this ratio by the small change, $\mathrm{d}u$, does not change its value. Hence, $\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y/\mathrm{d}u}{\mathrm{d}x/\mathrm{d}u}$, which rearranges to $\displaystyle \frac{\mathrm{d}y}{\mathrm{d}u}=\frac{\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)}{\left(\frac{\mathrm{d}u}{\mathrm{d}x}\right)}$. This is known as the Chain Rule. In your case, we set $u=(x^2)$ and have $\displaystyle\frac{\mathrm{d}y}{\mathrm{d}(x^2)}=\frac{\frac{\mathrm{d}y}{\mathrm{d}x}}{\frac{\mathrm{d}(x^2)}{\mathrm{d}x}}=\frac{1}{2x}\frac{\mathrm{d}y}{\mathrm{d}x}$ by the Power Rule.
You should be able to use this to explain what happens with higher powers. But whether the result is 'trivial' or not is simply a matter of perspective. Hopefully this explains your question in the comments about where the factor of $\frac{1}{2x}$ arises from. A small change in $x$ corresponds to a large change in $x^2$ **, which means the slope of $y$ with respect to $x^2$ must have a larger run than the slope with respect to $x$. Therefore, $\frac{\mathrm{d}y}{\mathrm{d}(x^2)}<\frac{\mathrm{d}y}{\mathrm{d}x}$.
Explanation 2: Composite Functions
The previous explanation might be conceptually easier but it is logically problematic. For one reason, how is a "small" change, $\mathrm{d}x$, actually defined? And how can we divide by something approximately zero, let alone justify a nonzero ratio between two approximately zero quantities? I personally think the meaning of $\frac{\mathrm{d}y}{\mathrm{d}(x^2)}$ also becomes quite murky and difficult to parse due to the small change reliant on a small change.
This can be remedied by conceptualising the problem in terms of functions, which justifies how the aforementioned variables, $y, u$ and $x$ are interrelated. Then the derivative of a function can be expressed as a second function that the first is transformed into.
Re-define $y$ and $u$ as the functions $y(x)=(f\circ u)(x)$ and $u(x)$, where we have written the composition $f(u(x))$ as a distinct function, $(f\circ u)(x)$. We can now state the chain rule as
$$\frac{\mathrm{d}y}{\mathrm{d}u}=\frac{\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)}{\left(\frac{\mathrm{d}u}{\mathrm{d}x}\right)} \quad\mapsto\quad f'(u(x))=\frac{(f\circ u)'(x)}{u'(x)}$$
With $u(x)=x^2$, we have $u'(x)=2x$ so therefore, $\displaystyle\frac{\mathrm{d}y}{\mathrm{d}(x^2)}= f'(x^2)=\frac{(f\circ u)'(x)}{2x}=\frac{y'(x)}{2x}$. This gives explains what we found before but also provides another, arguably clearer meaning to $\displaystyle\frac{\mathrm{d}y}{\mathrm{d}(x^2)}$, i.e. $f'(x^2)$, where $f(x)=y(\sqrt{x})$.
* The precise meaning of 'very small' is discussed elsewhere, under 'infinitesimal change'. I've given some sources to read further below.
** The opposite is true for when $x\approx 0$, in which case the corresponding chain in $x^2$ is small and the argument is reversed.
Credit to Jake Binnema - Secant Slope Calculator for the image.
Further reading:
-
On an entirely different note, looking graphically, $\frac{dy}{dx^2}$ would mean change in y corresponding to an infinitesimal change in $x^2$ How does the result equal the change in y corresponding to an infinitesimal change in x times some factor? Does this lend a physical meaning to itself? – Rew Dec 01 '19 at 15:08
-