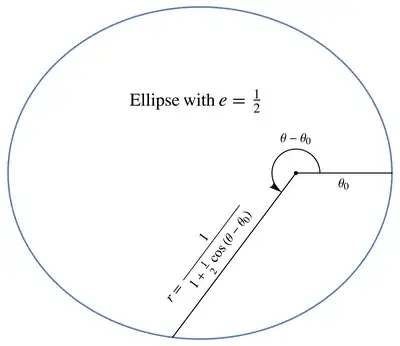
I am reading "Key Points of Mechanics" by Haruo Yoshida.
He wrote $r$ was a function of $\theta$. (please see below.)
But if $\theta(t_0)=\theta(t_1)$ and $r(t_0) \neq r(t_1)$ for $t_0 \neq t_1$, $r$ is not a function of $\theta$.
Please explain why $r$ is a function of $\theta$.
The equations of motion in a polar coordinate system are the following:
$m (\ddot{r}-r\dot{\theta}^2) = f_r$,
$m(r\ddot{\theta}+2\dot{r}\dot{\theta})=f_{\theta}$.If $f_r := -\frac{GMm}{r^2}, f_{\theta}:=0$, then
$\ddot{r}-r\dot{\theta}^2 = -\frac{GM}{r^2}$,
$r\ddot{\theta}+2\dot{r}\dot{\theta}=0$.$\frac{d}{dt}(r^2\dot{\theta}) = 2r\dot{r}\dot{\theta}+r^2\ddot{\theta} = r(r\ddot{\theta}+2\dot{r}\dot{\theta})=0$.
So, $r^2\dot{\theta}$ is constant.
Let $h := r^2\dot{\theta}$.$\ddot{r}-r\dot{\theta}^2 = \ddot{r}-r(\frac{h}{r^2})^2 = \ddot{r}-\frac{h^2}{r^3} = -\frac{GM}{r^2}$.
$r$ is a function of $\theta$ and the following equation holds:
$\frac{d}{d\theta}(\frac{1}{r^2}\frac{dr}{d\theta})=\frac{1}{r}-\frac{GM}{h^2}$.