Sum of the series $\sum_{n=0}^{\infty} \lfloor n\sqrt{2} \rfloor x^n$?

Question

Can we find the sum of the series $\sum_{n=0}^{\infty} \lfloor n\sqrt{2} \rfloor x^n$ explicitly? The question is related to this one where sum is computed if $\sqrt{2}$ is replaced by some rational number $r$.

Answer 1

This isn't a solution but it does yield a representation that has a nice approximation built into it. Note the series representation $$\left\lfloor x \right\rfloor =x-\frac{1}{2}+\frac{1}{\pi }\sum\limits_{k=1}^{\infty }{\frac{\sin \left( 2\pi kx \right)}{k}}$$
And so $${{B}_{1}}\left( \left\{ x \right\} \right)=\left\{ x \right\}-\frac{1}{2}=x-\left\lfloor x \right\rfloor -\frac{1}{2}=-\frac{1}{\pi }\sum\limits_{k=1}^{\infty }{\frac{\sin \left( 2\pi kx \right)}{k}}$$ Where ${{B}_{1}}$is a Bernoulli polynomial and $\left\{ x \right\}$ is the fractional part of $x$. Substituting and evaluating some series we have $$\sum\limits_{n=1}^{\infty }{\left\lfloor an \right\rfloor {{x}^{n}}}=\frac{ax}{{{\left( x-1 \right)}^{2}}}+\frac{1}{2\left( x-1 \right)}-\sum\limits_{n=0}^{\infty }{{{B}_{1}}\left( \left\{ an \right\} \right){{x}^{n}}}$$ Taking say the first term we get a good approximation

$$\sum\limits_{n=1}^{\infty }{\left\lfloor an \right\rfloor {{x}^{n}}}\simeq \frac{ax}{{{\left( x-1 \right)}^{2}}}+\frac{1}{2\left( x-1 \right)}+\frac{1}{2}$$

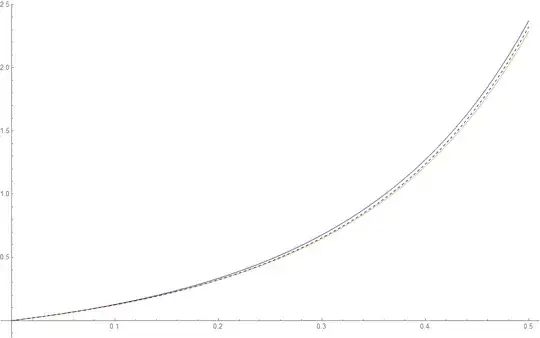
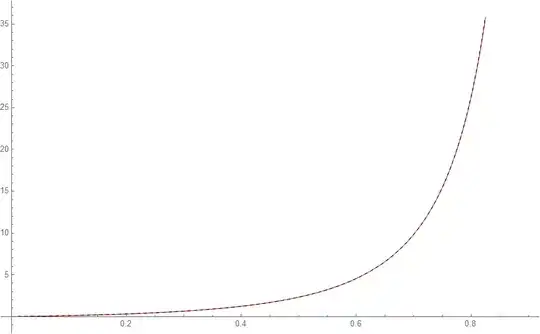
For $a=\sqrt{2}$ quick graphs highlight how reasonable the approximations indeed are. The first graph below shows the numerical evaluation of the series (black dashed), against the Bernoulli polynomial approximation for $n=0,1$ and $n=0,1,2$ (blue and orange respectively), over half the domain so as to highlight the discrepancy. The second graph shows the $n=0$ approximation over a wider domain.