In this function:
$$f(z) = \log(z-1) - \log(z+1)$$
it seems to me like there is only one option for the branch cut for this problem, between $z=1$ and $z=-1$ but I’m seeing other resources that indicate that there are several options.
On page 13 of this resource it indicates that there is more than one option for the branch cut.
Here’s my logic:
- since $z=1$ and $z=-1$ are the only two branch points
- and since we must draw branch cuts such that it is impossible to draw a circle around any one branch point without crossing the branch cut
- and since $z=\infty$ is not a branch point
- then it seems to me like the line connecting $z=1$ and $z=-1$ is the only option for the branch cut.
But this resource indicates that there are these two options for branch cuts:
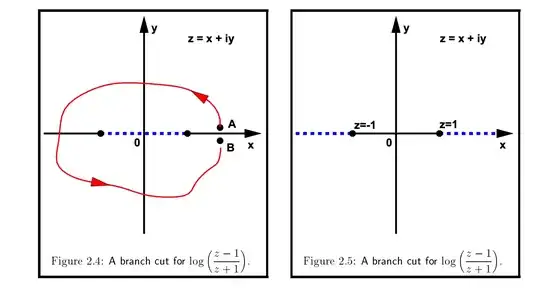 $f(z)=\log(z+1)-\log(z-1)$">
But I don’t understand why the rightmost option is even an option. There’s no branch point at $z=\infty$
$f(z)=\log(z+1)-\log(z-1)$">
But I don’t understand why the rightmost option is even an option. There’s no branch point at $z=\infty$