How $dxdy$ becomes $rdrd\theta$ during integration by substitution with polar coordinates

Question

Does anyone know how $dxdy$ becomes $rdrd\theta$ in the example below? I always end up with cosines and sines in the expression no matter how I go about it and I'm not sure how they are disappearing from the expression.

Answer 1

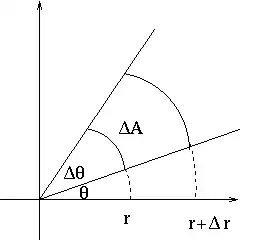
The answers using the Jacobian are (of course) correct. You can get some intuition from this picture:

$\Delta A$ is (approximately) a rectangle with sides $r \Delta \theta$ and $\Delta r$. Its area is proportional to $r$ since it scales as $r$ increases.

Picture from http://citadel.sjfc.edu/faculty/kgreen/vector/block3/jacob/node4.html

Answer 2

We are using polar coordinates that is

• $x=r \cos \theta$
• $y=r \sin \theta$

and by the Jacobian determinant we have that

$$dxdy=\begin{vmatrix}\cos\theta&-r\sin\theta\\\sin \theta&r\cos\theta\end{vmatrix}drd\theta=rdrd\theta$$

Refer also to the related

• What is the Jacobian matrix?
• Origin of Jacobian determinant

Answer 3

Perhaps seeing the two compared will help.

$\underline{\bf\text{1D Case:}}$

$$ \int_{a}^{b}f(x)dx=\int_{\alpha}^{\beta}f(x(u))\frac{dx}{du}du $$

$\underline{\bf\text{2D Case:}}$

$$ \iint_{D}f(x,y)dxdy=\iint_{D’}f(x(u,v),y(u,v))\Bigl\vert\frac{\partial{(x,y)}}{\partial{(u,v)}}\Bigr\vert{}dudv $$

As for where the actual matrix comes from:

When we transformed our coordinates from Cartesian to polar, we also transformed the differential elements $dx$ and $dy$. By doing this, we are no longer guaranteed that they are perpendicular; therefore, we are no longer guaranteed that $da=dxdy$. To find our true $da$, let's consider the following equations:

$$ \begin{align} dx&=\frac{\partial{x}}{\partial{r}}dr+\frac{\partial{x}}{\partial{\theta}}d\theta\\ dy&=\frac{\partial{y}}{\partial{r}}dr+\frac{\partial{y}}{\partial{\theta}}d\theta \end{align} $$

or

$$ \begin{pmatrix} dx\\ dy \end{pmatrix} = \bbox[yellow,5px] { \begin{pmatrix} \partial{x}/\partial{r} & \partial{x}/\partial\theta\\ \partial{y}/\partial{r} & \partial{y}/\partial\theta \end{pmatrix} } \begin{pmatrix} dr\\ d\theta \end{pmatrix}\\ \text{The highlighted matrix ends up being the Jacobian Matrix.} $$

This shows us the form that the basis vectors take under the transformation. Previously, we had $\overrightarrow{dx'}=dx\hat{e}_x= \begin{pmatrix} 1\\ 0 \end{pmatrix} dx\, $ and $\,\overrightarrow{dy'}=dy\hat{e}_y= \begin{pmatrix} 0\\ 1 \end{pmatrix} dy $ , with $da=\Vert{\overrightarrow{dx'}\times\overrightarrow{dy'}}\Vert=dxdy$ . However, now we have $\overrightarrow{dx}= \begin{pmatrix} \partial{x}/\partial{r}\\ \partial{y}/\partial{r} \end{pmatrix} dr $ and $\overrightarrow{dy}= \begin{pmatrix} \partial{x}/\partial\theta\\ \partial{y}/\partial\theta \end{pmatrix} d\theta $ , with $$da=\Vert{\overrightarrow{dx}\times\overrightarrow{dy}}\Vert=\bbox[yellow,5px]{\Bigl(\frac{\partial{x}}{\partial{r}}\frac{\partial{y}}{\partial{\theta}}-\frac{\partial{x}}{\partial{\theta}}\frac{\partial{y}}{\partial{r}}\Bigr)}drd\theta\text{.}\\ \frac{\partial{x}}{\partial{r}}=\cos\theta\,\text{,}\,\frac{\partial{y}}{\partial{\theta}}=r\cos\theta\,\text{,}\,\frac{\partial{x}}{\partial{\theta}}=-r\sin\theta\,\text{,}\,\frac{\partial{y}}{\partial{r}}=\sin\theta\,\text{, so the highlighted portion equals }r\text{.}\\ \therefore{} da=\Vert{\overrightarrow{dx}\times\overrightarrow{dy}}\Vert=rdrd\theta $$ Also notice that this highlighted quantity is equal to the determinant of the previously highlighted matrix. Again, it turns out that this is what we call the Jacobian Matrix, and calculating the Jacobian Determinant uncovers how the coordinate transformation affected the differential area element.

$$ \frac{\partial{(x,y)}}{\partial{(u,v)}}= \begin{vmatrix} \partial{x}/\partial{u} & \partial{x}/\partial{v}\\ \partial{y}/\partial{u} & \partial{y}/\partial{v} \end{vmatrix} =\frac{\partial{x}}{\partial{u}}\frac{\partial{y}}{\partial{v}}-\frac{\partial{x}}{\partial{v}}\frac{\partial{y}}{\partial{u}} $$

Answer 4

Taylor series mandate $dx^2=0$, from which you can show $dxdy=-dydx$ etc. (Look up the wedge product on differential fotms.) Thus$$\begin {align}dxdy&=(\cos\theta dr-r\sin\theta d\theta)(\sin\theta dr+r\cos\theta d\theta)\\&=r(\cos^2\theta+\sin^2\theta)drd\theta.\end{align}$$In particular, the $drd\theta$ coefficient is a determinant called the Jacobian.

Note, however, the calculation $ds^2=dx^2+dy^2=dr^2+r^2d\theta^2$ takes infinitesimals as commuting, because this time there's no nilpotency axiom, so we're not working with the wedge product on differential forms.

Answer 5

(I don't have enough rep to leave a comment, sorry)

To my knowledge, the Jacobian matrix represents the best approximation (differential) of our Cartesian points represented as polar coordinates. When you find its determinant, you are finding how the Jacobian scales area/volume.

Answer 6

Differential element has area

$dA= dx \cdot dy$ in Cartesian system for a rectangle and

$dA= r d\theta \cdot dr$ in Polar coordinates for the trapezium.

Evaluation of Jacobian matrix $((u_x,u_y), (v_x,v_y))$ leaves a multiplier of just $r,$ between $[(u,v)-(x,y)]$ systems.