5

Background

We know that the integral $\int f(x)~dx$ represents the area under the curve, where the area is represented by the sum of individual areas of elemental strips of the width $dx$ and height $f(x)$. As $dx$ is infinitesimal, we can ignore the error due to the curvature of the curve, and treat the elemental strips as almost 1-dimensional. As the curvature disappears at infinitesimal scale, the area becomes that of a perfect rectangle, $dx \times f(x)$.

enter image description here

Similarly, this can be extended to working out the volume of revolution, which consists of elemental "disks" of the face area $\pi f^2(x)$ and length $dx$. The name "disk" used in textbooks is really a cylinder with a large face area relative to a small (really, infinitesimal) length. The volume of a cyliner is equal to a face area $\times$ length, so the volume of revolution is $\int \pi f^2(x)~dx$. Again, this ignores the curvature of the original curve $f(x)$ and assumes that at each $dx$ the elemental unit is perfectly cylindrical.

The above are uncontroversial established textbook results.

Question

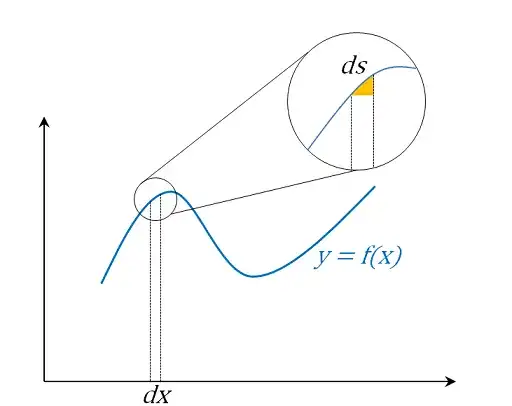
Why can't we extend the same principles in deriving the surface of revolution? If we take the cylinder as the elemental shape, the surface of revolution of the whole curve could be represented by the sum of lateral surfaces of the elemental cylinders, each equal to $2\pi f(x)\times dx$. So the whole surface would be equal to $\int 2\pi f(x)~dx$. But apparently this is wrong.

Instead, here, the textbook derivations (example) do take account of the curvature in $f(x)$, and use the elemental surface area equal to $2\pi f(x) \times ds$, where $ds$ is the curved length of the curve in each interval of $dx$. Hence, the elemental shape assumed is that of a tube, instead of a cylinder.

Why is it not acceptable to ignore the curvature here, but is acceptable in the calculations of area under the curve and volume of revolution?

Mihail
  • 245
  • Those are uncontroversial non-standard textbook results. There's no such thing as an infinitesimal in standard analysis, using infinitesimals means you're doing non-standard analysis ;-) – Daniel Fischer Nov 25 '19 at 14:11
  • @DanielFischer, OK, I have used standard in a colloquial sense. – Mihail Nov 25 '19 at 14:13
  • 1
    More to the point, for the integral or the volume of revolution, not only the curvature, also the slope is (or, "can be") ignored. For an arc-length or a surface of revolution, you must take the slope into account, but you can still ignore the curvature. – Daniel Fischer Nov 25 '19 at 14:15
  • @DanielFischer I have used curvature as a catch-all term that includes both non-linear and linear curvature (slope). Can you explain why is it important to differentiate between the two? It sounds like this is maybe the source of my confusion. – Mihail Nov 25 '19 at 14:20
  • 1
    Usually, curvature is a measure of the "change of slope" (caution, handwaving; look up the definition if you want it more precise). A straight line (segment) has curvature $0$ regardless of its slope. – Daniel Fischer Nov 25 '19 at 14:38
  • @HansLundmark thank you, the answers there address my question exactly! – Mihail Nov 25 '19 at 15:15

1 Answers1

1

Let's take the revolution part out of it and just consider length of a curve. What is the length of the line segment from $(0,0)$ to $(1,1)$?, If we follow your method, we should be able to do this:

  • For each n, divide the interval $[0,1]$ into $n$ pieces of equal width $\Delta x = \frac{1}{n}$.
  • For each $i$ from $0$ to $n$, approximate the curve over the interval $\left[\frac{i-1}{n},\frac{i}{n}\right]$ by the horizontal line segment connecting $\left(\frac{i-1}{n},\frac{i-1}{n}\right)$ to $\left(\frac{i}{n},\frac{i-1}{n}\right)$. The length of this line segment is $\frac{1}{n}$.
  • The length of the curve is approximately $$ \frac{1}{n} + \frac{1}{n} + \dots + \frac{1}{n} = 1 $$ Since the approximating sum does not depend on $n$, the length is precisely $1$.

But we know the actual length of this line segment is $\sqrt{1+1} = \sqrt{2}$. We must take the vertical displacement into account as well.

Matthew Leingang
  • 26,112
  • I understand this, but it doesn't quite address my question. I can see the sense in accounting for the curvature. But this contrasts with the established results I have described in the Background, where we are taught that it is acceptable to ignore the curvature at infinitesimal scale, as it becomes negligible. These are the two things I cannot reconcile. – Mihail Nov 25 '19 at 14:57