Results
I have not found a closed form of $s$. However, I will show below that the sum
$$s = \sum_{k=1}^{\infty} (-1)^{k+1}\frac{\left\lfloor \sqrt{k}\right\rfloor}{k}\tag{1}$$
has the following integral representation
$$s_i = \int_0^1 f(x) \, dx\tag{2a}$$
where the integrand is defined as
$$f(x) = \frac{1-\vartheta _4(0,x)}{2 x (x+1)}\tag{2b} $$
Here
$$\vartheta _4(u,q) = 1 + 2 \sum_{n=1}^{\infty} (-1)^n q^{n^{2}} \cos(2 n u)\tag{3}$$
is a Jacobi theta function $[1]$.
The integrand of $s_i$ looks pretty harmless
Derivation
We start by writing down a list of summands of $s$ long enough to see a pattern
$$s\simeq \left\{1,-\frac{1}{2},\frac{1}{3},-\frac{2}{4},\frac{2}{5},-\frac{2}{6},\frac{2}{7},-\frac{2}{8},\frac{3}{9},-\frac{3}{10},\frac{3}{11},-\frac{3}{12},\frac{3}{13},-\frac{3}{14},\frac{3}{15},-\frac{4}{16},\frac{4}{17},-\frac{4}{18}\right\}$$
We see that the list can be decomposed into sublists
$$s_1= \left\{1,-\frac{1}{2},\frac{1}{3}\right\}$$
$$s_2= \left\{-\frac{2}{4},\frac{2}{5},-\frac{2}{6},\frac{2}{7},-\frac{2}{8}\right\}= 2 \left\{-\frac{1}{4},\frac{1}{5},-\frac{1}{6},\frac{1}{7},-\frac{1}{8}\right\}$$
$$s_3= \left\{\frac{3}{9},-\frac{3}{10},\frac{3}{11},-\frac{3}{12},\frac{3}{13},-\frac{3}{14},\frac{3}{15}\right\}= 3 \left\{\frac{1}{9},-\frac{1}{10},\frac{1}{11},-\frac{1}{12},\frac{1}{13},-\frac{1}{14},\frac{1}{15}\right\}$$
Notice that the denominators of the sublist $s_1$ runs from $1$ to $3$, of $s_2$ from $4$ to $8$,of $s_3$ from $9$ to $15$ resp., in general of sublist $s_m$ from $m^2$ to $(m+1)^2-1=m(m+2)$.
To express the pattern formally we use the alternating harmonic sum defined as
$$A(n) = \sum _{k=1}^n \frac{(-1)^{k+1}}{k}\tag{4}$$
Then we can write
$$s_1 = A(3),\\ s_2 = 2 (A(8) -A(3)),\\ s_3 = 3(A(15) - A(8)) $$
and for the partial sums
$$p_1 = s_1 = A(3), \\p_2 = s_1+s_2 = 2 A(8) -A(3), \\p_3 = p_2+s_3 = 3 A(15) - A(8)-A(3)$$
the general partial sum of index $m$ is then
$$p_{m} = m A((m+1)^2-1) - \sum_{k=2}^{m} A(k^2-1)\tag{5}$$
Observing now that
$$A(n) = \sum_{k=1}^n (-1)^{k+1}\int_0^1 x^{k-1}\,dx= \int_0^1 \sum_{k=1}^n (-1)^{k+1} x^{k-1}\,dx= \int_0^1 \frac{1-(-1)^n x^n}{x+1} \, dx\tag{6}$$
we get
$$p_{m} =\int_0^1 \left( \frac{m \left((-1)^{m (m+2)} x^{m (m+2)-1}+1\right)}{x+1}-\sum _{k=2}^m \frac{(-1)^{k^2} x^{k^2-1}+1}{x+1}\right) \,dx\tag{7}$$
Without changing the value we can extend the second sum down to $k=1$. Now we observe that the contribution $\frac{m}{1+x}$ cancels out and that the parity of $k^2$ is the same as that of $k$ and similarly $m(m+2) \sim m$ so that we have
$$p_{m} = \int_0^1 \left(\frac{m \left((-1)^{m} x^{m (m+2)}\right)}{x(x+1)}-\sum _{k=1}^m \frac{(-1)^{k} x^{k^2}}{x(x+1)}\right) \,dx\tag{8}$$
Now we need the limit $m\to\infty$ to get $s=\lim_{m\to \infty } \, p_{m}$.
The first integral is given by
$$I_1(m) = m (-1)^m \int_0^1 \frac{x^{m (m+2)}}{x (x+1)} \, dx\\=\frac{1}{2} (-1)^m m \left(\psi ^{(0)}\left(\frac{1}{2} (m+1)^2\right)-\psi ^{(0)}\left(\frac{1}{2} m (m+2)\right)\right)\tag{9}$$
For $m>>1$ we find that $I_1 \sim \frac{(-1)^m}{2 m}$ so that it vanishes in the limit.
For the limit of the second integral
$$I_2(m) = -\int_0^1 \sum _{k=1}^m \frac{(-1)^{k} x^{k^2}}{x(x+1)} \,dx\tag{10}$$
we have to calculate the sum of the integrand up to $m\to\infty$. Observing $(3)$ we obtain $(2)$. QED.
Discussion
Honestly speaking, I didn't expect to find an integral representation because I thought that sharply discontinuous aggregates like $\left\lfloor x\right\rfloor$ would not lead to a smooth formula. But, luckily, my feelings turned out to be misleading, and I was pushed forward by the rather straightforward derivation itself.
Series expansion of the integrand
The list of terms of the series expansion of the integrand starts like this
$$f(x) = \left\{1,-x,x^2,-2 x^3,2 x^4,-2 x^5,2 x^6,-2 x^7,3 x^8,-3 x^9,3 x^{10},-3 x^{11},3 x^{12},-3 x^{13},3 x^{14},-4 x^{15}\right\}$$
When integrated
$$s=\int_0^1 f(x) \,dx \simeq \left\{1,-\frac{1}{2},\frac{1}{3},-\frac{1}{2},\frac{2}{5},-\frac{1}{3},\frac{2}{7},-\frac{1}{4},\frac{1}{3},-\frac{3}{10},\frac{3}{11},-\frac{1}{4},\frac{3}{13},-\frac{3}{14},\frac{1}{5},-\frac{1}{4}\right\}$$
we get back where we started from.
This gives me some comfort because I felt a little uneasy about the general validity of the limit while selecting the special form of the partial sums
- We have in fact found an integral representation also for the sum
$$h = \sum_{k=1}^{\infty} (-1)^{k+1}\frac{\sqrt{k}-\left\lfloor \sqrt{k}\right\rfloor}{k}$$
because the trivial part is
$$\sum _{k=1}^{\infty } \frac{(-1)^{k+1}}{\sqrt{k}}=-\left(\sqrt{2}-1\right) \zeta \left(\frac{1}{2}\right)\simeq 0.604899$$
- Accuracy
The accuracy issue is briefly that - roughly speaking - Mathematica gives a different numerical result for the integral with NIntegrate than for the sum with NSum. I believe that the value obtained with NIntegrate is better because the integrand is alsmost trivial (see the graph). We had a similar topic recently here.
In the meantime, Yuriy S in a comment has given this numerical value for the integral $(2)$ with Mathematica's NIntegrate, and WorkingPrecision -> 30
$$i_{Yuriy} = 0.591560779349817340213846903345$$
I can confirm this result.
I have calculated the sum with NSum and different values of WorkingPrecision. The results are wobbling appreciably about the limiting value as can be seen in the picture
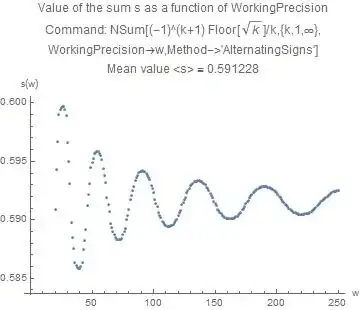
And I can ony give this very modest result (the average)
$$s_{WH,NSum} = 0.59123$$
Alternatively, the plain Sum of the first million terms is
$$s_{WH,Sum} = 0.5910$$
The accuracy is but $\frac{1}{\sqrt{k_{max}}} \simeq 10^{-3}$
River Li in his solution $[2]$ has transformed the limiting form of the sum $(5)$ into the better converging double sum
$$s_{RL} = \log(2) + \sum_{n=1}^\infty (-1)^n n
\sum_{i=1}^{n} \frac{1}{(n^2 + 2i-1)(n^2+2i)}$$
The n-summand has a closed form in terms of polygamma functions and goes asymptotically like $\frac{1}{n^2}$. Hence the convergence is similar to that of Dirichlet $\eta(2)$.
Mathematica finds 5 valid digits for $s_{RL}$ with 1000 n-summands in a few seconds, but refuses to sum 2000 terms is acceptable time.
However, River Li found twenty digits using Maple, a result he later confirmed using the
"Convergence Acceleration methods for Alternating Sums" as described here $[3]$ with only 28 terms. This method claims that you can get high precision results from just a few tens of terms. Usage of the method is nicely described in the update of River Li's solution.
Hence I conclude that using summation to find the value of the sum with high accuracy as requested in problem b) needs sophisticated summation methods which provide convergence acceleration, accompanied by a good SC-tool.
Here we are lucky to have the integral representation of the sum for which Mathematica delivers as many digits as requested.
- Generalization
If we consider the similar problem with the p-th root instead of the square root we have
$$s(p) = \sum _{k=1}^{\infty } \frac{(-1)^{k+1} \left\lfloor k^{1/p}\right\rfloor }{k} = \int_{0}^{1} f(p,x)\,dx$$
where now the integrand is given by
$$f(p,x)=\frac{\sum _{m=1}^{\infty } (-1)^{m-1} x^{m^p}}{x (x+1)}$$
I know no name for this special function which replaces the Jacobi theta function.
The problem with a rational exponent $\frac{p}{q}$ with $1 \lt p\lt q$ seems to be much more difficult to tackle.
- Using Fourier expansion
We can get rid of the floor function using the Fourier series
$$\left\lfloor x\right\rfloor = x -\frac{1}{2} + \frac{1}{\pi}\sum_{k=1}^{\infty} \frac{\sin(2 \pi k x)}{k}\tag{5.1}$$
@Jam has pursued this approach in https://math.stackexchange.com/a/3452471/198592, and ended with this sum to be evaluated
$$d=-\frac{1}{\pi}{\sum_{n\geq 1}\sum_{k\geq 1}\frac{\left(-1\right)^{n}\sin\left(2\pi k\sqrt{n}\right)}{nk}}\tag{5.2}$$
We can do the $k$-sum
$$\sum_{k\geq 1} \frac{\sin\left(2\pi k\sqrt{n}\right)}{k}=
\frac{i}{2}\left(\log \left(1-e^{2 i \pi \sqrt{n}}\right)-\log \left(1-e^{-2 i \pi \sqrt{n}}\right)\right) \\
= \frac{1}{2} i \log \left(\frac{1-e^{2 i \pi \sqrt{n}}}{1-e^{-2 i \pi \sqrt{n}}}\right)\\
=\frac{1}{2} i \log \left(-e^{2 i \pi \sqrt{n}}\right)\tag{5.3}$$
Here is another expression for d
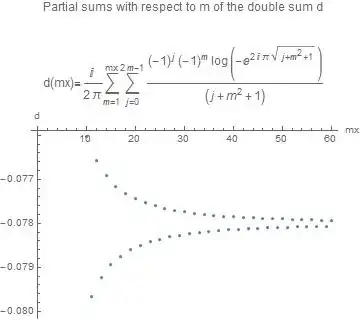
$$d_{nsq}=\frac{i}{2\pi }\sum _{m=1}^{\infty }(-1)^m \sum _{j=1}^{2 m} (-1)^j\frac{ \log \left(-e^{2 i \pi \sqrt{j+m^2}}\right)}{ \left(j+m^2\right)}\tag{5.10}$$
The convergence is satisfactory as can be seen from the following graph
References
$[1]$ http://mathworld.wolfram.com/JacobiThetaFunctions.html
$[2]$ https://math.stackexchange.com/a/3450665/198592
$[3]$ https://people.mpim-bonn.mpg.de/zagier/files/exp-math-9/fulltext.pdf



WorkingPrecision->30:0.591560779349817340213846903345, which seems to fit well between approximate values0.588 - 0.595which I've got by summing20000terms of the original series using "half the last term" correction. Very nice answer. – Yuriy S Nov 25 '19 at 20:02