I think it's actually less trouble to prove Tonelli's theorem
(which I imagine in this context means something like
Theorem 8.43 of Apostol, Mathematical Analysis (2nd ed. 1974),
although the more general* proposition (5.3.6) of
Dieudonné, Foundations of Modern Analysis (1969) could also be used)
than it is to prove this result without using Tonelli's theorem!
However, nothing daunted $\ldots$
*Minor correction (not needed for this argument): it isn't strictly
accurate to describe Dieudonne's (5.3.6) as more general than
Apostol's Theorem 8.43. I listed some other references in a comment
on this related question.
Define the triangular numbers:
$$
t_k = \frac{k(k+1)}{2} \quad (k \geqslant 0),
$$
and the infinite sequence $(b_r)_{r\geqslant0}$, where:
$$
b_r = a_k \quad (k \geqslant 0,\ t_k \leqslant r < t_{k+1}),
$$
thus:
$$
\begin{array}{c|ccccccccccc}
r & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & \cdots \\
b_r & a_0 & a_1 & a_1 & a_2 & a_2 & a_2 & a_3 & a_3 & a_3 & a_3 & \cdots
\end{array}
$$
For $N \geqslant 0$, define the $(t_{N+1})^\text{th}$
partial sum of the series $\sum_{r=0}^\infty b_r$, thus:
$$
s_N = \sum_{r=0}^{t_{N+1}-1}b_r = \sum_{k=0}^N(k+1)a_k
\quad (N \geqslant 0).
$$
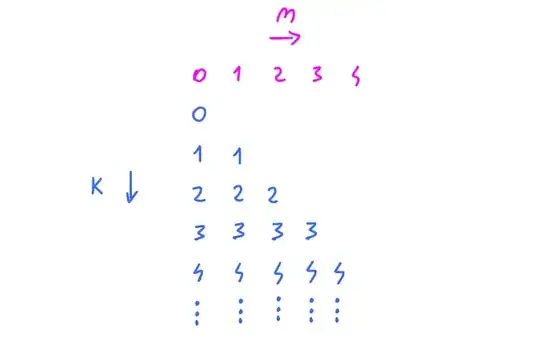
Consider this infinite triangular array:
$$
\begin{array}{c|ccccc}
\vdots & \vdots & \vdots & \vdots & \vdots & \\
\text{row } 3 & & & & b_9 & \cdots \\
\text{row } 2 & & & b_5 & b_8 & \cdots \\
\text{row } 1 & & b_2 & b_4 & b_7 & \cdots \\
\text{row } 0 & b_0 & b_1 & b_3 & b_6 & \cdots \\
\hline
\text{sums} & a_0 & 2a_1 & 3a_2 & 4a_3 & \cdots
\end{array}
$$
The $n^\text{th}$ row of the array is the infinite sequence
$\big(c_k^{(n)}\big)_{k\geqslant{n}}$, where:
$$
c_k^{(n)} = b_{t_k + n} = a_k \quad (k \geqslant n \geqslant 0).
$$
In terms of the $c_k^{(n)}$, the selected partial sums of the series
$(b_r)_{r\geqslant0}$ are given by:
$$
s_N = \sum_{n=0}^N\sum_{k=n}^Nc_k^{(n)} \quad (N \geqslant 0).
$$
For $N \geqslant n \geqslant 0$, the $(N-n)^\text{th}$ remainder of
the infinite series $\sum_{k=n}^{\infty}c_k^{(n)}$ is the sum of a
subsequence of $(b_r)$ whose indices satisfy $r\geqslant{t_{N+1}}$.
For $n > N \geqslant 0$, the entire infinite series
$\sum_{k=n}^{\infty}c_k^{(n)}$ is the sum of such a subsequence of
$(b_r)$. Also,
$$
t_k + n \ne t_{k'} + n'
\quad (k \geqslant n \geqslant 0, \ k' \geqslant n' \geqslant 0,
\ n \ne n').
$$
This means that all the series just mentioned are the sums of
pairwise disjoint subsequences of the sequence $(b_r)$ with
indices $r\geqslant{t_{N+1}}$.
Now we begin to consider questions of convergence. It is required
to prove:
$$
\sum_{n=0}^\infty \sum_{k=n}^{\infty} a_k =
\sum_{n=0}^{\infty} (n+1)a_n,
$$
where $a_n \geqslant 0$ for all $n$. This is trivial if $a_n = 0$
for all $n$, so we assume from now on that $a_n > 0$ for some $n$,
whence the sums on either side of the identity, if well-defined, are
also strictly positive. If the iterated infinite sum on the left
hand side is well-defined and equal to $S > 0$, then $S$ is an
upper bound for all the finite sums:
$$
\sum_{n=0}^N\sum_{k=n}^N a_k = \sum_{n=0}^N(n+1)a_n
\quad (N \geqslant 0),
$$
whence the infinite sum on the right hand side of the conjectured
identity is also well-defined.
It is therefore enough to prove that if the sum on the right hand
side of the identity is well-defined and equal to $S > 0$, then the
iterated sum on the left hand side of the identity is also
well-defined and equal to $S$.
Given $\epsilon > 0$, choose $N$ so that:
$$
\sum_{r=t_{N+1}}^\infty b_r = \sum_{n=N+1}^\infty(n+1)a_n
\leqslant \epsilon.
$$
Lemma
Let $m$ be an integer, and let
$(b_r)_{k \geqslant m}$ be a sequence of non-negative numbers such
that $\sum_{r=m}^\infty b_r$ converges. For any infinite set
$$
L = \{l(0), l(1), l(2), \ldots\} \text{ where }
m \leqslant l(0) < l(1) < l(2) < \cdots,
$$
define
$$
\sigma(L) = \sum_{i=0}^\infty b_{l(i)}.
$$
Then for any infinite sequence of pairwise disjoint infinite subsets
$L_0, L_1, L_2 \ldots$ of $\{r \in \mathbb{Z} : r \geqslant m\}$ we
have
$$
\sum_{n=0}^\infty \sigma(L_n) \leqslant \sum_{r=m}^\infty b_r.
$$
Proof
In the contrary case, there are $\eta > 0$ and an integer $M \geqslant 1$ such that
$$
\sum_{n=0}^{M-1} \sigma(L_n) = \sum_{r=m}^\infty b_r + 2\eta.
$$
From $L_n$ ($n = 0, 1, \ldots, M-1$) take enough terms of the series
for $\sigma(L_n)$ to give a partial sum greater than
$\sigma(L_n) - \eta/M$. By the disjointness condition, all these
terms together have a sum greater than
$$
\sum_{n=0}^{M-1} \sigma(L_n) - \eta > \sum_{r=m}^\infty b_r,
$$
which is a contradiction.
The lemma shows that the $(N-n)^\text{th}$ remainder of
the infinite series $\sum_{k=n}^{\infty}c_k^{(n)}$ for
$n = 0, 1, \ldots, N$, together with the entirety of the series
$\sum_{k=n}^{\infty}c_k^{(n)}$ for $n = N+1, N+2, \ldots$,
form an infinite series whose sum is at most $\epsilon$.
Denote this by $\sum_{n=0}^\infty d_n$. Then:
$$
\sum_{n=0}^N\sum_{k=n}^\infty c_k^{(n)} =
\sum_{n=0}^N\left(\sum_{k=n}^N c_k^{(n)} + d_n\right) =
\sum_{n=0}^N\sum_{k=n}^N c_k^{(n)} + \sum_{n=0}^N d_n,
$$
therefore:
$$
\sum_{n=0}^\infty\sum_{k=n}^\infty a_k =
\sum_{n=0}^\infty\sum_{k=n}^\infty c_k^{(n)} =
\sum_{n=0}^N\sum_{k=n}^N c_k^{(n)} + \sum_{n=0}^\infty d_n
= s_N+ \sum_{n=0}^\infty d_n.
$$
This shows that the iterated sum on the left hand side of the
conjectured identity is well-defined, and its value lies between
$s_N$ and $s_N + \epsilon$. The two sides of the identity therefore
differ by most $\epsilon$. Since $\epsilon$ was arbitrary, this
proves that they are equal.