Proof of closed-form solution of the difference of two factorial series

Question

Context

I'm working on a problem tangentially related to the Kepler Equation 1. The details are very much in the weeds, and I'm not in a position to explain at this time exactly how I have arrived at Equation 1. Yet, I believe that the following holds true: $$ \lim_{k\rightarrow \infty} \sum\limits_{s=0}^{ k- 1 } \, \dfrac{ \left[ 2^{ 2\,(k- s) } \left[ ( k- s) !\right]^4 - \pi\,2^{2(s-k) -1 } \, \left[ 2\,(k - s)]!\right]^2 [ 2\,(k -s) ] \right] }{[2(k- s)]![2\,(k- s) ]\,\left[ ( k - s) ! \right]^2} = \dfrac{ \pi }{2 } - 1 ~\text{Eq}.~1.$$

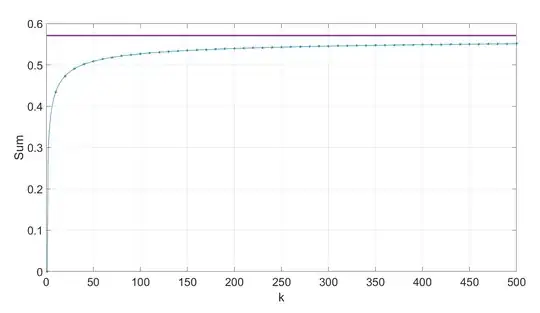
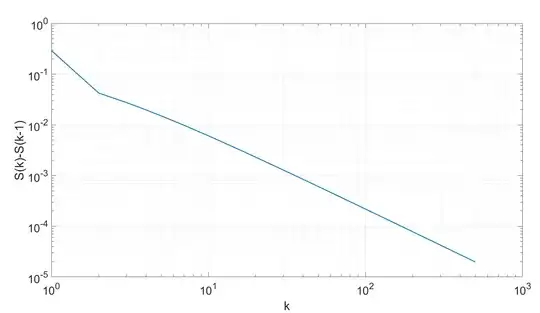
I've plotted Equation 1 for various $k$. My results seem to indicate that the expression above is plausibly true. Beyond $k=50$ I run into floating point issues in the numerical calculation, and series is not computable.

I cannot figure out how to determine the veracity of the equation 1. I've seen some closed-form solutions to factorial series (e.g., [2]).[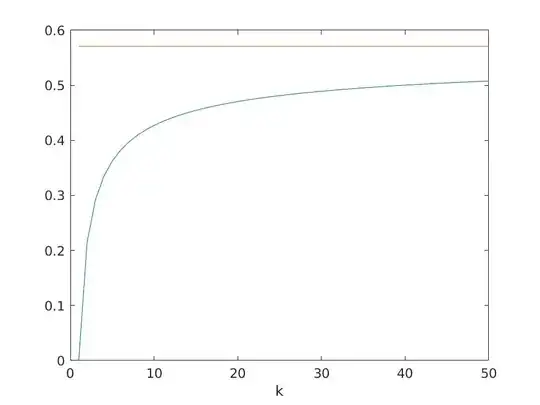] Yet, I have not seen such an expression elsewhere.

Questions

1. Does anyone have one or more references to a book that has many factorial series?

2. Can anyone prove Equation 1 true or false?

3. Can anyone illustrate the results for $k >> 50$?

Bibliography

1 Find the inverse of an equation reminiscent of Kepler's equation

[2] http://mathworld.wolfram.com/FactorialSums.html

Answer 1

Here is the sum evaluated to 500 as well as a plot of the difference between successive terms, FYI.

HTH

Answer 2

Rewriting,

$\begin{array}\\ f(k) &=\sum\limits_{s=1}^{ k } \, \dfrac{2^{2s}(s!)^4 - \pi\,2^{-2s-1} (2s)!^2(2s)} {2s(2s)!(s!)^2}\\ &=\sum\limits_{s=1}^{ k } \, \dfrac{2^{2s}(s!)^4 } {2s(2s)!(s!)^2} -\pi\sum\limits_{s=1}^{ k } \, \dfrac{2^{-2s-1} (2s)!^2(2s)} {2s(2s)!(s!)^2}\\ &=\sum\limits_{s=1}^{ k } \, \dfrac{2^{2s-1}(s!)^2 } {s(2s)!} -\pi\sum\limits_{s=1}^{ k } \, \dfrac{2^{-2s-1} (2s)!} {(s!)^2}\\ &=f_1(k)-\pi f_2(k)\\ \lim_{k \to \infty} f(k) &=\dfrac{\pi}{2 } - 1 ~\text{Eq}.~1.\\ \end{array} $

According to Wolfy,

$f_1(k) = \dfrac{(2^{2 k + 1} (2 k + 1) ((k + 1)!)^2)}{((k + 1) (2 (k + 1))!)} - 1 $ and $f_2(k) = \dfrac14\dfrac{(4^{-k} (k + 1) (2 (k + 1))!}{(k + 1)!^2} -\dfrac12 $.

Now, take limits (left to you).

Answer 3

Starting from @marty cohen's answer and fimplifying, we have $$f_1(k)=\sqrt{\pi }\,\frac{ \Gamma (k+1)}{\Gamma \left(k+\frac{1}{2}\right)}-1$$ $$f_2(k)=\frac{\Gamma \left(k+\frac{3}{2}\right)}{\sqrt{\pi }\, \Gamma (k+1)}-\frac{1}{2}$$ $$f_1(k)-\pi f_2(k)=\frac \pi 2-1+\sqrt \pi\left(\frac{\Gamma (k+1)}{\Gamma \left(k+\frac{1}{2}\right)}-\frac{\Gamma \left(k+\frac{3}{2}\right)}{\Gamma (k+1)} \right)$$ Now, using Stirling approximation and continuing with Taylor series for large values of $k$ $$\log \left(\frac{\Gamma (k+1)}{\Gamma \left(k+\frac{1}{2}\right)}\right)=\frac{1}{2} \log \left({k}\right)+\frac{1}{8 k}-\frac{1}{192 k^3}+O\left(\frac{1}{k^5}\right)$$ $$\frac{\Gamma (k+1)}{\Gamma \left(k+\frac{1}{2}\right)}=t+\frac{1}{8 t}+\frac{1}{128 t^3}-\frac{5}{1024 t^5}+O\left(\frac{1}{t^7}\right)$$ where $\color{red}{t=\sqrt k}$.

Similarly $$\log \left(\frac{\Gamma \left(k+\frac{3}{2}\right)}{\Gamma (k+1)}\right)=\frac{1}{2} \log \left({k}\right)+\frac{3}{8 k}-\frac{1}{8 k^2}+\frac{3}{64 k^3}-\frac{1}{64k^4}+O\left(\frac{1}{k^5}\right)$$ $$\frac{\Gamma \left(k+\frac{3}{2}\right)}{\Gamma (k+1)}=t+\frac{3}{8 t}-\frac{7}{128 t^3}+\frac{9}{1024 t^5}+O\left(\frac{1}{t^7}\right)$$ $$f_1(k)-\pi f_2(k)=\frac \pi 2-1+\sqrt \pi\left(-\frac{1}{4 t}+\frac{1}{16 t^3}-\frac{7}{512t^5}+O\left(\frac{1}{t^7}\right)\right)$$

Computing for $k=10$, the exact value is $$f_1(10)-\pi f_2(10)=\frac \pi 2-1+\frac{215955}{46189}-\frac{707825 \pi }{524288}\approx 0.4340968$$ while the above expansion gives $$\frac{\pi }{2}-1-\frac{12487 }{51200}\sqrt{\frac{\pi }{10}}\approx 0.4340980$$

With regard to @user3113647's plots, we then have $$S(k)-S(k-1)=\frac{1}{8} \sqrt{\pi } \left(\frac{1}{k}\right)^{3/2}+O\left(\frac{1}{k^{7/2}}\right)$$ and then a slope of $-\frac 32$ in the logarithmic scale.