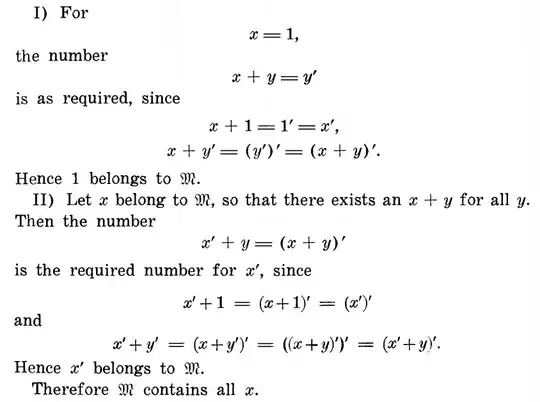He uses an inductive proof here. To be specific, on the outside, he does induction on $x$, and shows that $x$ has the desired property for any $y$.
Part I of his proof is of course the inductive base $x=1$ for this proof. That is, he shows that for $x=1$ there exists a number with the desired property given any $y$.
Part II is the inductive step. Here, he shows that if for some $x$ there exists some number $x+y$ that has the desired property given any $y$, then for $x'$, there exists some number $x'+y$ that has the desired property given any $y$.
In particular: the inductive hypothesis is that for some $x$ it is true that:
1) $x+1=x'$
2) $x+y'=(x+y)'$
And he uses that to prove:
1) $x'+1=x'$
2) $x'+y'=(x'+y)'$
So, when you say:
Isn't this similar to what we are trying to prove? namely: $x+y'=(x+y)'$
He assumes $x+y'=x+y$, but he is trying to show that $x'+y'=(x'+y)'$. Those are similar, yes, but they are (crucially!) not the same.
Did he assumed it? If so, why are we allowed to that?
Yes: he assumed $x+y'=(x+y)'$, but yes: he is allowed to do so, since that is the nature of inductive proofs.
Hope that helps!