Here is the official theorem I'll use: 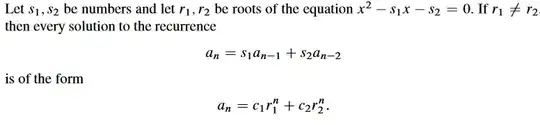
Since the Fibonacci sequence is defined as $F_n=F_{n-1}+F_{n-2}$, we solve the equation $x^2-x-1=0$ to find that $r_1 = \frac{1+\sqrt 5}{2}$ and $r_2 = \frac{1-\sqrt 5}{2}$
So we have $F_n = c_1\left(\frac{1+\sqrt 5}{2}\right)^n + c_2\left(\frac{1-\sqrt 5}{2}\right)^n$
We know that $F_0 = F_1 = 1$. So we can solve the following system to find the values of $c_1$ and $c_2$:
$1 = c_1 + c_2$
$1 = c_1\left(\frac{1+\sqrt 5}{2}\right) + c_2\left(\frac{1-\sqrt 5}{2}\right)$
Solving this system does not give $c_1 = 1/\sqrt5, c_2 = -1/\sqrt 5$ , even though that is apparently the right answer, i.e. the closed form of the Fibonacci sequence is apparently $$\frac1{\sqrt 5}\left(\frac{1+\sqrt 5}{2}\right) -\frac1{\sqrt 5}\left(\frac{1-\sqrt 5}{2}\right)$$
Where did I go wrong? Why doesn't solving the system of equations give me $c_1 = 1/\sqrt5, c_2 = -1/\sqrt 5$?