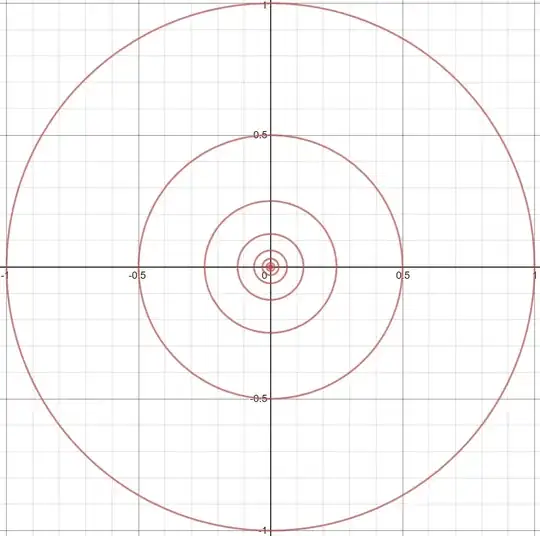
I experimented with mathematics and Mathematica and got a very interesting curve, which defined as: $$\sqrt{x^{2}+y^{2}}=\cos\left(\log_{2}\left(\sqrt{x^{2}+y^{2}}\right)\right)$$ After plotting this equation, we get infinite concentric circles(whose radius is less than or equal to one). It looks like a circle equation: $\sqrt{x^{2}+y^{2}}=R$
Questions:
- How to works a right part of first equation?
- How to modify a first equation for getting sequence of radiuses: $\frac{1}{1}$,$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,$\frac{1}{16}$,...
- Can we call it a recursive or a fractal object?