Mise en abyme is per definition a formal technique of placing a copy of an image within itself, often in a way that suggests an infinitely recurring sequence. The image below represents the technique:
And we know from mathematics that a fractal is a never-ending pattern.
The question is; are fractals mise en abyme?
No, but...
Whenever one is tempted to ask the question "Are fractals [___]?", the answer is almost certainly "No," unless the question can refined and made more explicit. This is, in large part, due to the fact that the term "fractal" does not even have a formal mathematical definition. I've written about this issue before on MSE, so I won't repeat myself here. The important take-away is that the collection of objects which we might like to call "fractals" is a large and nebulous collection. Any question which asks about some shared property of all fractals is likely to have an unsatisfactory answer.
However, there is still hope for a more satisfactory answer under more constrained hypotheses. The asker here seems to have keyed in on the self-similar structure of certain fractal sets.[1] Essentially, and without getting into too much detail, some fractal sets can be constructed by iteratively "shrinking" an initial set, making several copies of that initial set, and "gluing them together" in some manner. For example, the von Koch curve can be constructed by taking an interval, shrinking it by a factor of $1/3$, making four copies, and gluing them together:
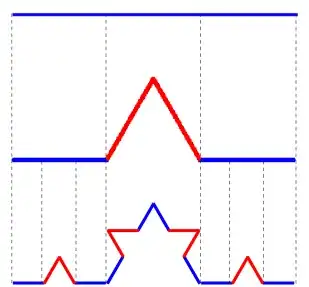
There is a nice description of this process at Larry Ridddle's website, which is the source of the above image. The set obtained at the end of this process is self-similar: if you take this limiting set, shrink it by the appropriate factor, make the right number of copies, and glue them together correctly, the result is the original limiting set.
It is, however, worth noting that not every self-similar set is fractal (as the word fractal is typically understood). For example, the unit interval $[0,1]$ is self-similar: shrink the interval by a factor of $1/2$, make two copies, and glue them together end-to-end. The result is, again, the unit interval.
In this setting, it might be reasonable to say that a self-similar set is a mise en abyme. However, I think that even this might be overreaching a little. As I understand the term, mise en abyme refers to a technique used in art—the term implies a dynamic process, the end result of which is a static image. In contrast, a fractal is typically understood to be a static object (a set), and not a process.
I think that the most correct phrasing would be the following:
Self-similar sets, which are often (but not always) fractal may be generated or rendered via the technique of mise en abyme.
[1] Wikipedia has a page on self-similar sets, though the page is, I think, somewhat confusing in that it conflates self-similarity, statistical and/or approximate self-similarity, and self-affinity into a single concept. Unfortunately, a quick Googling didn't turn up any better descriptions for a non-technical audience. The seminal paper on the topic is probably Hutchinson's:
Hutchinson, John E., Fractals and self similarity, Indiana Univ. Math. J. 30, 713-747 (1981). ZBL0598.28011.
