Closed form for functional equation $g(x)=\frac{1}{2}(g(x^2)+g((1-x)^2))$ on $[0,1]$

Question

See bottom for edit to question:

Before providing background, my question is if there is a closed-form solution to

$$g(x)=\frac{1}{2}(g(x^2)+g((1-x)^2))$$

with $g(0)=g(1)=0$ and $g(1/2)=1$. If this can not be found, can it at least be proven that the solution is unique. A further question I have that I have not been able to show is that $g(x)$ is increasing on $[0,1/2)$ and decreasing on $(1/2,1]$.

This is an offshoot of the question here. It was initially asked if the functions defined

$$f_0(x)=x(1-x)$$

$$f_n(x)=\frac{1}{2}(f_{n-1}(x^2)+f_{n-1}((x-1)^2))$$

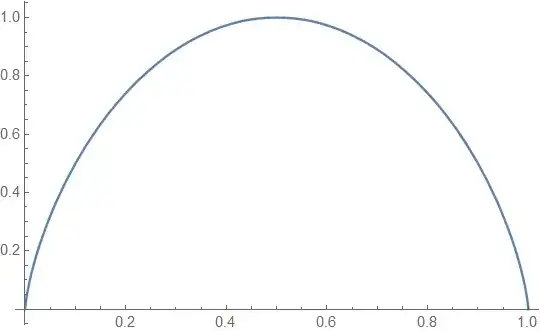
are increasing on $[0,1/2]$ and decreasing on $[1/2,0]$. For example, $\frac{f_{10}(x)}{f_{10}(1/2)}$ is given by the graph

However, it seems that whatever function $f_n(x)$ is approaching is universal up to a constant regardless of $f_0(x)$ (provided $f_0(x)$ is continuous on $[0,1]$). For example, if $f_0(x)=\sin(2\pi x)$, then $f_{15}(x)$ looks like

This then led to a conjecture: That for any continuous $f_0(x)$ on $[0,1]$, $f_n(x)$ approaches

$$a_ng(x)+b_n$$

where $a_n,b_n$ are constants and $g(x)$ is the solution to

$$g(x)=\frac{1}{2}(g(x^2)+g((1-x)^2)).$$

with $g(0)=g(1)=0$ and $g(1/2)=1$. Note that I do not have a proof that these conditions on $g(x)$ produce a unique solution, but it seems likely from testing. The reason that the constants do not matter in $ag(x)+b$ is that for $h(x)=ag(x)+b$

$$g(x)=\frac{1}{2}(g(x^2)+g((1-x)^2))$$

$$ag(x)+b=a\frac{1}{2}(g(x^2)+g((1-x)^2))+b$$

$$h(x)=\frac{1}{2}(ag(x^2)+b+ag((1-x)^2)+b)$$

$$h(x)=\frac{1}{2}(h(x^2)+h((1-x)^2))$$

and therefore $h(x)$ also satisfies the functional relation.

Some properties of a solution $g(x)$ are:

$1)\ g(x)=g(1-x)$

$2)\ g^{(n)}(1)=(-1)^n g^{(n)}(0)$

$3)\ g^{(n)}(0)=g^{(n)}(0)=0\text{ for }n>1$

This is found differentiating $g(x)$ and the functional equation and then plugging in $x=1$. For example, for $n=2$, we get

$$g''(1)=2 g''(1)+g'(0)+g'(1)$$

However, since we know $-g'(0)=g'(1)$, this simplifies to

$$g''(1)=2g''(1)\Rightarrow g''(1)=g''(0)=0 $$

This can be extended by induction to all $n>1$.

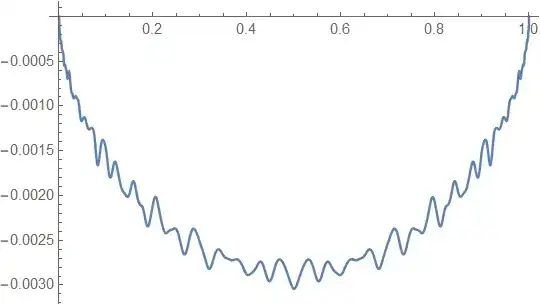
EDIT: As was pointed out in the comments, the only reason the parabola-like curve appears is that $f_n(x)$ was normalized by $f_n(1/2)$ with that in mind, what can we say about the limit of

$$\frac{f_n(x)}{f_n(1/2)}$$

as $n$ goes to infinity. Does this curve have a shape? If so, does this shape have a closed form solution?

Answer 1

There is no continuous solution to this functional equation. Indeed, suppose such a $g$ was continuous. Then it achieves a maximum value at some $t\in[0,1]$. We then must have $g(t)=g(t^2)$ since $g((1-t)^2)\leq g(t)$, and then similarly $g(t^2)=g(t^4)=g(t^8)=\dots$. By continuity we conclude $g(t)=g(0)=0$ which is a contradiction since $g(1/2)=1$.

Note that because of your normalization where you divide by $f_n(1/2)$, the function that your graphs approach would instead be a solution to $$cg(x)=\frac{1}{2}(g(x^2)+g((1-x)^2))$$ where the constant $c$ is the limiting value of $f_{n+1}(1/2)/f_n(1/2)$.