0

my question is somewhat related to this one here, where the expected value of the distance $d$ of two uniformly drawn points from an interval $[0;L]$ is sought. It's $\frac{L}{3}$ and the pdf should be $f(d)=\frac{2}{L^2}(L-d)$ if I'm not mistaken.

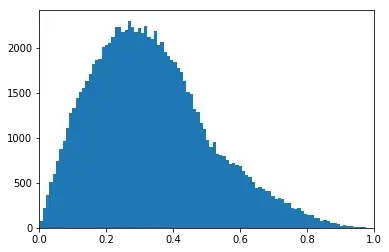
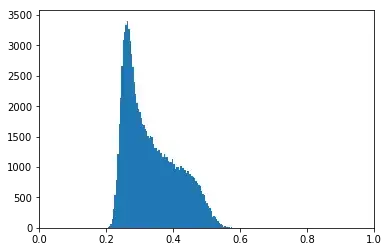
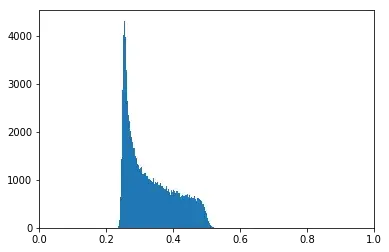
Now imagine we're drawing $N+1$ points from the interval and designate one as the reference $y$. I'd like to know how the average distance to $y$ is distributed, i.e. $\frac{1}{N}\sum|x_n-y|=\frac{1}{N}\sum{d_n}\sim\;?$

For $N=1$ we have the situation from above, but for larger $N$ I don't know how to derive this because the pdf's of the individual distances are not independent. Is it even possible to get an analytic formulation? I looked at some histograms for different $N$ and how they seem to be "evolving" in a non-trivial manner ($N=[1,2,10,100,1000]$)

N=1

N=2

N=10

N=100

N=1000

Any help in understanding this behaviour is much appreciated!

Jens Petersen
  • 105

1 Answers1

1

mechanically writing out the answer using Dirac delta function notation, the probability density function of the squared distance, $d^2$, is $$p(d^2)=\frac{1}{L^{N+1}}\int_0^Ldy\int_0^Ldx_1...\int_0^L d_{x_N}\delta \left( d^2-\frac{1}{N}\sum{(y-x_n)^2}\right)$$ and integrating the delta function is possible by taking limit of integral of delta function limiting form (Gaussian or tent/box of constant area in the limit of its width going to zero). for instance, using Lorentzian limiting form, we have $$p(d^2)=\lim_{\epsilon \to 0}\frac{1}{\pi L^{N+1}}\int_0^Ldy\int_0^Ldx_1...\int_0^L d_{x_{N}}\frac{\epsilon}{ \left( d^2-\frac{1}{N}\sum{(y-x_n)^2}\right)^2+\epsilon^2}$$

Jens Petersen
  • 105
phdmba7of12
  • 1,030
  • 1
    Great idea with the Dirac approach. My integration skills aren't really that advanced, do you think that there is a closed-form solution? – Jens Petersen Nov 13 '19 at 13:22
  • glad you think it is a great idea (feel free to upvote)... back in graduate school, during my dissertation, ran across a similar complex set of nested integrals involved delta functions and ended up using symbolic solver Maple to obtain closed-form expressions – phdmba7of12 Nov 13 '19 at 17:21
  • or $$p(d^2)=\lim_{\epsilon \to 0}\frac{1}{2 \epsilon L^N}\int_0^Ldx\int_0^Ldx_1...\int_0^L d_{x_{N-1}}\Theta \left( \left| d^2-\frac{1}{N-1}\sum{(x-x_i)^2}-\epsilon\right| \right)$$ where $\Theta(x)$ is Heaviside step function – phdmba7of12 Nov 13 '19 at 18:20