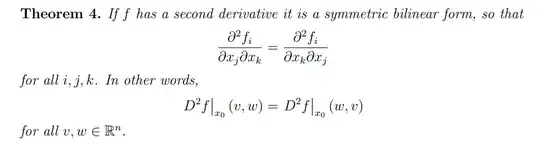I'm reading a note about higher derivative:
and a remark
The remark said that "The proof below does NOT assume continuity of the second derivative."
From my textbook and Wikipedia, I got that the necessary condition for the second derivative to be symmetric is that it is continuous, contradicting the above remark.
Could you please explain elaborate on this discrepancy? Thank you for your help!
Here is the proof in the note: