Let $a > 0$. Show that the sequence defined by $$ x_0 = 1, \qquad x_{n+1} = a^{x_n} $$ converges for $a \leq e^{1/e}$.
Any help is appreciated, I don't even know where to start with this.
Edit to add clarifications:
The case $1 \leq a \leq e^{1/e}$ is solved below in the comments and answers. It is also easy to show that the sequence does not converge for $a > e^{1/e}$ (not part of the question but still worth mentioning).
The interesting case is the remaining one $0 < a < 1$. Here, I found that $x_{n-1} < x_n \Rightarrow x_n > x_{n+1}$ so that the sequence seems to be oscillating. Since $x_0 > x_1$, this implies that the subsequence $\{x_{2n}\}$ is decreasing while the subsequence $\{x_{2n+1}\}$ is increasing, and both converge since they are bounded. This is illustrated by the plot below of the first few terms of the sequence when $a = 0.1$.
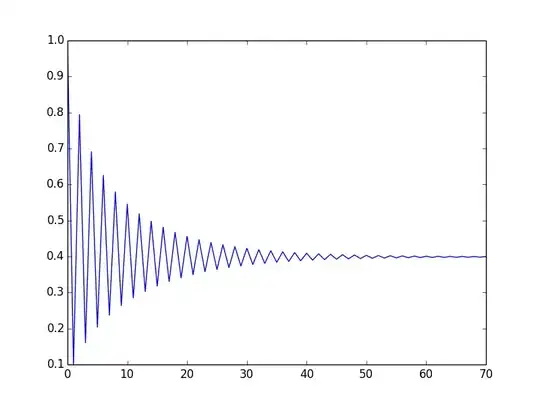
It remains to show that both subsequences have the same limit, which is where I have trouble.