0

  • $\sqrt{1+x} - \sqrt{1-x}$ is a subtractive cancellation when $x \approx 0$, and

  • $1 - \cos(x)$ is a catastrophic cancellation when $x \approx \pi$.

I've been trying to read up on it but can't seem to click. They both make very $\pi$ like numbers but are different cancellation? How do they differ? Could someone please explain it to me?

Rodrigo de Azevedo
  • 1
bobby
  • 111
  • 1
  • 6
  • What does "Catasphrohic" mean? – bof Nov 07 '19 at 07:41
  • One way to define catastrophic cancellation is to look at power series expansions and check whether some terms cancel out. In both your examples the highest order term of the expansions cancels out. This does not happen in your second example, as $\cos(x)$ is close to $-1$ for $x$ close to $\pi$? – quarague Nov 07 '19 at 07:46
  • Is your second expression originally $1+\cos(x)$? Else it is rather stable around $x=\pi$. – Lutz Lehmann Nov 07 '19 at 10:55
  • This answer addresses the root of your problem. – Carl Christian Nov 07 '19 at 20:12
  • @Dr.LutzLehmann Ohh I misread the question I copied down. It's unstable when $x \approx 0$ and the alternate formula made using the conjugate is unstable when $x \approx \pi$ src: https://gyazo.com/0981f1544244d75ab8a26f2f0d9313c7 – bobby Nov 07 '19 at 22:09

2 Answers2

1

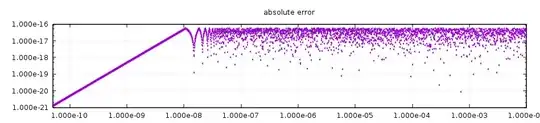
The terms in the first expression have floating point errors of about $(1+|x|)\mu$ where $\mu$ is the machine constant, $1{\rm ulp}$ or relative precision of the floating point data type. So in the difference you get errors of up to $2(1+|x|)\mu$. However, the exact value of the expression is, by binomial expansion, $\frac{2x}{\sqrt{1+x}+\sqrt{1-x}}$, which for small $x$ is about $x$. Thus the relative error close to $x=0$ will be large.

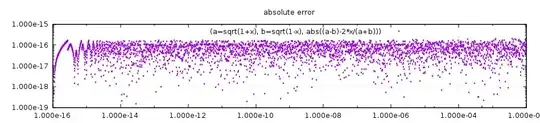
plot of absolute difference of the two expressions

The same happens with the second expression, if it were $1+\cos(x)$. The floating point error of the sum, which effectively is a subtraction, is bounded by $(1+|\cos(x)|)\mu\le 2\mu$, while the equivalent expression $\frac{\sin^2(x)}{1-\cos(x)}$ shows that the difference can become arbitrarily small. For $|x-\pi|<\sqrt{\mu}$ the original expression will evaluate as zero, giving relative error $1$, which is slightly more catastrophic than in the first task where that happens only for $|x|<\mu$.

plot of absolute difference of the two expressions

Lutz Lehmann
  • 126,666
0

I guess it is because the first difference is of the order $x$, while the second one is of the order $(x-\pi)^2$ (from Taylor's expansion).

Sergey Guminov
  • 4,038