Prove $\zeta(3)=2\sum_{n=1}^\infty\frac{H_n}{n}\left[\frac1{4^n}{2n\choose n}\left(H_{2n}-H_n-\frac1{2n}-\ln2\right)+\frac1{2n}\right]$

Question

How to prove

$$\zeta(3)=2\sum_{n=1}^\infty\frac{H_n}{n}\left[\frac1{4^n}{2n\choose n}\left(H_{2n}-H_n-\frac1{2n}-\ln2\right)+\frac1{2n}\right]$$

where $H_n$ is the harmonic number and $\zeta$ is the Riemann zeta function.

This problem is proposed by Cornel which can be found here and no solution has been submitted yet.

I know the following identity $$H_{2n}-H_n-\ln2=-\int_0^1\frac{x^{2n}}{1+x}dx$$ is related but I do not know how to exploit it.

I prefer a solution without calculating each sum separately because if we seperate, all these sums are calculated here but the first one $\sum_{n=1}^\infty\frac{H_nH_{2n}}{n4^n}{2n\choose n}$.

Answer 1

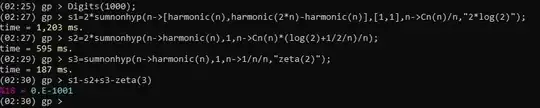
First lets break the problem into three series:

\begin{align} S&=2\sum_{n=1}^\infty\frac{H_n}{n}\left[\frac1{4^n}{2n\choose n}\left(H_{2n}-H_n-\frac1{2n}-\ln2\right)+\frac1{2n}\right]\\ &=2\sum_{n=1}^\infty \frac{H_n}{n4^n}{2n\choose n}\left(H_{2n}-H_n-\ln2\right)-\sum_{n=1}^\infty \frac{H_n}{n^24^n}{2n\choose n}+\sum_{n=1}^\infty\frac{H_n}{n^2}\\ &=2S_1-S_2+S_3 \end{align}

---

Calculating $S_1$

@Song proved here

$$\int_0^1\frac{x^{2n}\ln x}{\sqrt{1-x^2}}dx=\frac{\pi}2\frac{{2n\choose n}}{4^n}\left(H_{2n}-H_n-\ln 2\right)\tag1$$

Multiply both sides of (1) by $\frac{H_n}{n}$ then sum up from $n=1$ to $\infty$ we get

\begin{align} S_1&=\frac{2}{\pi}\int_0^1\frac{\ln x}{\sqrt{1-x^2}}\sum_{n=1}^\infty \frac{H_n}{n}x^{2n} dx\\ &=\frac{2}{\pi}\int_0^1\frac{\ln x}{\sqrt{1-x^2}}\left(\frac12\ln^2(1-x^2)+\operatorname{Li}_2(x^2)\right)dx\\ &=\frac1{\pi}\int_0^1\frac{\ln x\ln^2(1-x^2)}{\sqrt{1-x^2}}dx+\frac{2}{\pi}\int_0^1\frac{\ln x\operatorname{Li}_2(x^2)}{\sqrt{1-x^2}}dx \end{align}

The first integral can be evaluated using the beta function:

$$\int_0^1\frac{\ln x\ln^2(1-x^2)}{\sqrt{1-x^2}}dx=\frac{\pi}{2}\zeta(3)-2\pi\ln^32$$

and the second integral is elegantly calculated by Cornel here

$$\int_0^1\frac{\ln x\operatorname{Li}_2(x^2)}{\sqrt{1-x^2}}dx=\frac{5\pi}8\zeta(3)-\pi\ln2\zeta(2)+\pi\ln^32$$

Combine the two results we get $$\boxed{S_1=\frac74\zeta(3)-2\ln2\zeta(2)}$$

---

Calculating $S_2$

Using the well-known identity

$$\sum_{n=1}^\infty \frac{\binom{2n}n}{4^n}x^n=\frac{1}{\sqrt{1-x}}-1$$

Divide both sides by $x$ then integrate , we get

$$\quad\displaystyle\sum_{n=1}^\infty \frac{\binom{2n}n}{n4^n}x^n=-2\ln(1+\sqrt{1-x})+C $$
set $x=0,\ $ we get $C=2\ln2$

$$\sum_{n=1}^\infty \frac{\binom{2n}n}{n4^n}x^n=-2\ln(1+\sqrt{1-x})+2\ln2\tag2$$

Now multiply both sides of (2) by $-\frac{\ln(1-x)}{x}$ then integrate from $x=0$ to $1$ and use the fact that $-\int_0^1 x^{n-1}\ln(1-x)dx=\frac{H_n}{n}$ we get

\begin{align} S_2&=2\underbrace{\int_0^1\frac{\ln(1+\sqrt{1-x})\ln(1-x)}{x}dx}_{\sqrt{1-x}=y}-2\ln2\underbrace{\int_0^1\frac{\ln(1-x)}{x}dx}_{-\zeta(2)}\\ &=8\int_0^1\frac{y\ln(1+y)\ln y}{1-y^2}dy+2\ln2\zeta(2)\\ &=4\int_0^1\frac{\ln(1+y)\ln y}{1-y}-4\int_0^1\frac{\ln(1+y)\ln y}{1+y}+2\ln2\zeta(2) \end{align}

where the first integral:

$$\int_0^1\frac{\ln x\ln(1+x)}{1-x}\ dx=\zeta(3)-\frac32\ln2\zeta(2)$$

and the second integral:

$$\int_0^1\frac{\ln x\ln(1+x)}{1+x}\ dx=-\frac12\int_0^1\frac{\ln^2(1+x)}{x}dx=-\frac18\zeta(3)$$

Combine the results we get

$$\boxed{S_2=\frac92\zeta(3)-4\ln2\zeta(2)}$$

Finally, combine the boxed results of $S_1$ and $S_2$ along with $S_3=2\zeta(3)$, the closed form of $S$ follows.

---

Bonus:

We proved above that

$$S_1=\sum_{n=1}^\infty \frac{H_n}{n4^n}{2n\choose n}\left(H_{2n}-H_n-\ln2\right)=\frac74\zeta(3)-2\ln2\zeta(2)$$

So

$$\sum_{n=1}^\infty \frac{H_nH_{2n}}{n4^n}{2n\choose n}=\sum_{n=1}^\infty \frac{H_n^{2}}{n4^n}{2n\choose n}+\ln2\sum_{n=1}^\infty\frac{H_n}{n4^n}{2n\choose n}+\frac74\zeta(3)-2\ln2\zeta(2)$$

I managed here to prove

$$\sum_{n=1}^\infty \frac{H_n^{2}}{n4^n}{2n\choose n}=\frac{21}2\zeta(3)$$

$$\sum_{n=1}^\infty \frac{H_n}{n4^n}{2n\choose n}=2\zeta(2)$$

By collecting these results we get

$$\boxed{\sum_{n=1}^\infty \frac{H_nH_{2n}}{n4^n}{2n\choose n}=\frac{49}{4}\zeta(3)}$$

Answer 2

Naming $C_n(n)$ the normalized central binomial $\binom{2n}{n}\frac{1}{4^n}$, the following Pari/GP output provides the error between the sum and $\zeta(3)$.

$s_1=2\sum_{n=1}^\infty C_n(n) H_n [H_{2n}-H_n]/n$

$s_2=2\sum_{n=1}^\infty C_n(n) H_n [\log(2)+\frac{1}{2n}]/n$

$s_3=\sum_{n=1}^\infty H_n/n^2$

such that $s=s_1-s_2+s_3$. Using 1000 decimal digits the difference with $\zeta(3)$ is 0.