1

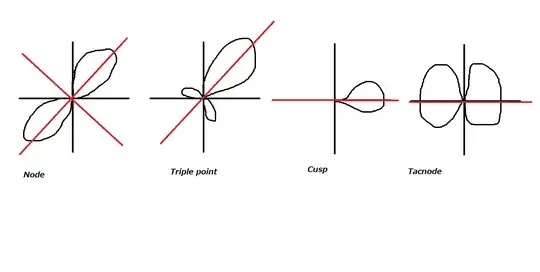
Q Which is which in Figure?

a)$x^2=x^4+y^4$

b)$xy=x^6+y^6$

c)$x^3=y^2+x^4+y^4$

d)$x^2y+xy^2=x^4+y^4$ enter image description here

a)$x^2=x^4+y^4$

This is invariant under the transformation $x\mapsto -x$ and $y\mapsto -y$. Thus it is Tacnode.

b)$xy=x^6+y^6$

It is invariant under the map $(x,y) \mapsto (y,x)$, thus Node or Triple point.

Because triple points meat the small circle of origin in six times and six is the degree of this polynomial, thus I guess this curve is triple point but I cannot prove it in some precise manner.

c)$x^3=y^2+x^4+y^4$

This curve is invariant under the map $y \mapsto -y$ and it is not invariant under the map $x \mapsto -x$, thus Cusp.

d)$x^2y+xy^2=x^4+y^4$

It is invariant under the map $(x,y) \mapsto (y,x)$, thus Node or Triple point.

Because triple points meat the small circle of origin in 4 times and 4 is the degree of this polynomial, thus I guess this curve is Node but I cannot prove it in some precise manner.

I cannot answer for cuves b) and d).

Jean Billie
  • 496

2 Answers2

1

For example: observe that

$$x^2=x^4+y^4\implies y^4=x^2(1-x)(1+x)$$

Now, which graph intersects the $\;x\,-$ axis thrice? Or also which graph has both $\;x\;$ and $\;y\;$ symmetry?

Now, if we write $\;f(x,y)=xy-x^6-y^6\;$ , then $\;f(-x,-y)=f(x,y)\;$

Taking $\;xy\neq0\;$ , we get that

$$xy=x^6+y^6\implies y=\frac{x^6+y^6}x\;\;\text{is an odd function of}\;\;x$$

and the same can be said of the above as a function of $\;y\;$ , so...This is also invariant under $\;(x,y)\to\pm (x,y)\;$ and $\;(x,y)\to\pm (y,x)\;$ .

DonAntonio
  • 211,718
  • 17
  • 136
  • 287
  • From the symmetry $(x,y) \to (-x,-y)$, $xy-x^6-y^6=0$ is Node, because triple point does not have this symmetry. But the degree is six and the triple point through the origin in six times, so I am not sure but the equation $xy-x^6-y^6=0$ should be triple point? – Jean Billie Nov 05 '19 at 12:25
1

Hint: The homogeneous term of lowest degree tells you the tangent directions at the origin. For instance, the lowest order term of $x^2 - x^4 - y^4 = 0$ is $x^2 = x \cdot x$, so the line $x=0$ is a double tangent line at the origin. Only one of your graphs has this property--can you see which one?

You can match the other graphs and equations similarly. Just zoom in on the portion of the graph near the origin and see what the tangent lines are.

Viktor Vaughn
  • 19,278
  • I know what you say is cusp. I cannot understand why the term indicates the tangent directions at origin. For example, the triple point has six distinct directions in the origin. Are this six directions revealed by the homogeneous term of lowest degree, namely the term $x^2y+y^2x$ in Equation $x^2y+y^2x=x^4+y^4$? – Jean Billie Nov 05 '19 at 11:22
  • I guess it relates the intersection of the blowing up and the exceptional curve. – Jean Billie Nov 05 '19 at 12:12
  • No, the cusp has $y=0$ (horizontal line) as a double tangent. Which one has the vertical line $x=0$ as a double tangent? – Viktor Vaughn Nov 05 '19 at 15:22
  • Every homogeneous polynomial in two variables splits into linear factors. Factoring $x^2y + y^2 x = xy(x+y)$ so the tangent lines are $x = 0$, $y = 0$, and $y = -x$. Each line contributes two directions. – Viktor Vaughn Nov 05 '19 at 15:24