Irrational exponents - complex roots - software handling of complex numbers

Question

When calculating $(-2)^{\pi}$ we get: $$ Z=(-2)^π=2^π (\cos(π^2(2k+1))+i \sin(π^2(2k+1))),\quad k \in \mathbb{Z} $$ at $k=0$: $$z=(-2)^π=2^π(\cos(π^2)+i \sin(π^2))$$

Now $z^{1/π}$ must be $-2$

no software can get -2 ... and I keep getting a wrong argument (or phase angle) although the abs is correct which is 2 as shown in the attached pic using julia programming language.

Does anyone have a good interpretation of that and how can we get the correct value?

Answer 1

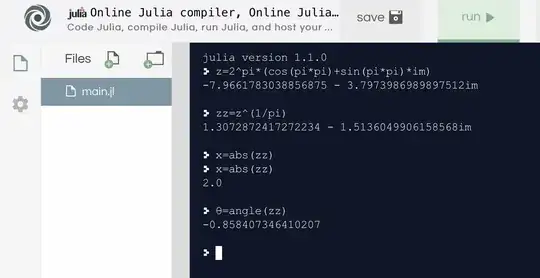
Now $z^{1/\pi}$ must be $−2$

Why? This intuition is often coming from the "rule" $(a^b)^c = a^{bc}$ but this only applies in special circumstances when dealing with complex-valued exponentiation. In fact, in this context, the cases where that equality holds would be more appropriately seen as the exception to the rule, rather than the rule itself.

As for what is happening here? It's just trigonometry. When you evaluate $$\cos(\pi^2)+i\sin(\pi^2) = \cos(\pi^2-4\pi)+i\sin(\pi^2-4\pi),$$ its principal angle is $\pi^2 - 4\pi,$ not $\pi^2.$ Then when you divide the angle by $\pi,$ you get $$\frac{\pi^2 - 4\pi}{\pi} = \pi - 4 \approx -0.858407346$$

---

As for your ultimate question of "how can we get the correct value?" I don't know if there is a way to systematically do it. In this case, you'd need to take the original exponent ($\pi$), multiply it by $\pi$ (to get $\pi^2$), and then find which branch this angle is in -- in this case, $$-\pi + 2k\pi < \pi^2 < \pi+2k\pi \implies k=2.$$ Then when you take the next power ($1/\pi$) you'd need to tell your program to use that branch rather than the principal branch.