1

I was wondering if this is a correct way to apply "exponent rules",

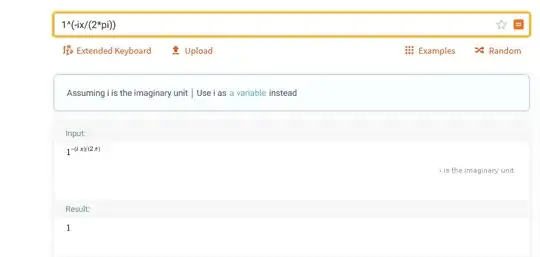
$$e^{x}=\left(e^{2\pi i}\right)^{x/2\pi i}=1^{-ix/2\pi}$$

I thought it was safe, just found it a bit weird, but I wanted to check if I could plot this in Wolfram Alpha and get the usual graph for $e^{x}$ (WA allows to plot both the real and imaginary parts of a real, complex valued function).

To my surprise the result appears to be 1.

So, did I make a mistake in applying these rules? or is Wolfram Alpha making a mistake?

EDIT: Here is an image (in case I'm right and it gets modified in the future).

Screenshot of the conondrum

2 Answers2

2

Yes this is a confusing thing. The property $(x^{a})^b=x^{ab}$ holds when $x$ is a positive real number and $a$ and $b$ are real numbers. More generally this property fails. This leads to many fake "proofs" like \begin{align} 1&=1^{1/2}\\ &=((-1)^2)^{1/2}\\ &=(-1)^{2/2}\\ &=\left(\left(-1\right)^{1/2}\right)^2\\ &=i^2\\ &=-1. \end{align}

With complex exponentiation, you have to be extra careful because expressions like $z^{1/n}$ are usually not well-defined. When you switch to complex numbers, for example, $16$ suddenly has $4$ fourth roots. So by convention, $\sqrt[4]{16}=2$, but the equation $z^4=16$ has the set of solutions $\{2,-2,2i,-2i\}$.

Also see the responses here.

pancini
  • 19,216
  • 4
    I guess you meant to say either $(x^a)^b=x^{ab}$ or $x^{a+b}=x^ax^b$ in the case when $x>0$. –  Oct 31 '19 at 02:31
  • In the fake proof above, the false statement used is that $(ab)^m=a^mb^m$ for negative $a,b.$ It's not clear how you intend for this to be an explanation of the anomaly in OP. – Allawonder Oct 31 '19 at 17:36
  • Sorry; I wrote one thing and then corrected only half of it. – pancini Oct 31 '19 at 17:53
1

The problem here is that the rule $$(a^m)^n=a^{mn},$$ which is true for positive $a\ne 1$ and real $m,n$ fails to be true when $m,n$ are nontrivially complex (that is, complex numbers with nonzero imaginary parts). The reason for this is that there are infinitely many ways to represent the same complex number in exponential form, because of the periodicity of the trigonometric functions. That is, we have that for any complex $z=re^{i\phi},$ we also have $$re^{i\phi}=re^{i\phi+2πki},$$ where $k$ can be any integer.

To see why this causes a problem for your example, we must have $$e^x=(e^{2πi})^{x/2πi}=(e^{2πki})^{x/2πi}=e^{kx},$$ which is obviously false.

So, again, the problem is with assuming that $(a^m)^n=a^{mn}$ is valid here. Thus, what we have is that $$e^x\ne (e^{2πi})^{x/2πi}.$$

Allawonder
  • 13,327
  • Isn't the first equation also valid for $a=1$? Both sides should be equal to 1, shouldn't they? –  Oct 31 '19 at 17:11
  • 1
    @SV It is, but we don't usually use $1$ as base, hence my neglect of it. Note I did not claim that it is false in that case. – Allawonder Oct 31 '19 at 17:32
  • Hahaha it is true, you never said it was not the case for 1, only that it was true for all other positive numbers. –  Oct 31 '19 at 17:39