6

Let $P:x\mapsto x^{10}-x^5-1$. The complex roots of $P$ form a regular convex pentagon with the middles of the sides thereof, hence the symmetry group of the considered set of points of the plane is the dihedral group of order $10$. Can one deduce from that that this group is the Galois group of $P$? If yes, can this be recovered from the fact that $P(x)=z^2-z-1$ with $z=x^5$, the symmetry group of the former being of order $2$ and the one of the latter for $z=a\neq 0$ being the cyclic group of order $5$?

enter image description here

Jyrki Lahtonen
  • 133,153
Sylvain Julien
  • 2,572
  • 1
    If you calculate the three roots furthest to the left, the one on the real axis is $-0.908244$, while the complex conjugate pair above and below it share a real part of $-0.890749$. – Jyrki Lahtonen Nov 01 '19 at 09:40
  • Is there a nice expression for the ratio of the absolute values of the two real roots? – Sylvain Julien Nov 01 '19 at 11:04
  • 1
    Call the positive real root $$\alpha=\left(\frac{1+\sqrt5}2\right)^{1/5}.$$ Then the negative real root is $-1/\alpha$. The ratio of their absolute values is $\alpha^2$, or the Golden ratio raised to power $2/5$. – Jyrki Lahtonen Nov 01 '19 at 11:38

1 Answers1

5

There are a few surprises in here. For many people actually, including yours truly!

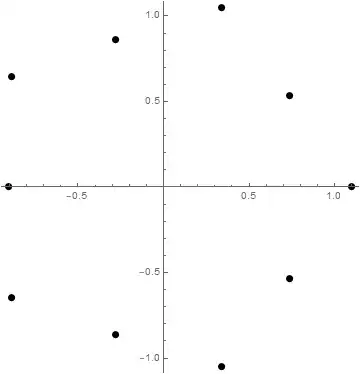
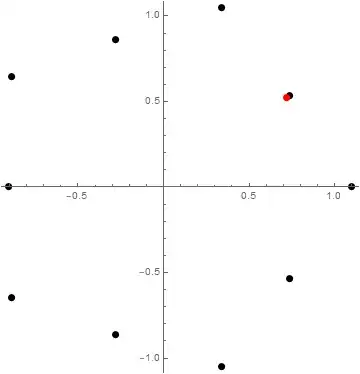
A surprise to you may be that, in spite of appearances to the contrary, one half of the roots are not exactly at the midpoints of that pentagon. Also sprach Mathematica:

the ten roots and an average of a pair of them

The red dot marks the midpoint of the two adjacent roots on the outer circle. Close, but no cigar.

But, you had me very worried for a moment. You see, $P(x)=x^{10}-x^5-1$ is irreducible over $\Bbb{Q}$ (I will add a proof later, if you want). And in characteristic zero an irreducible polynomial cannot have three roots in an arithmetic progression. I paid a bounty, even if a bit finicky, for a proof of that fact. And I also trust Ewan Delanoy :-)

Consequently the Galois group will also be bigger. If $\alpha$ is one of the roots of $P(x)$, the rest of them are $\alpha\zeta^k$, and $-\alpha^{-1}\zeta^k$ for $k=0,1,2,3,4$ and $\zeta=e^{2\pi i/5}$. So $L=\Bbb{Q}(\alpha,\zeta)$ is the splitting field. We have $[L:\Bbb{Q}]=20$. This is because $K=\Bbb{Q}(\alpha^5)=\Bbb{Q}(\sqrt5)$, and it is well known that $\zeta$ is quadratic over $K$.

Also, as $P(x)$ is irreducible, it follows that the Galois group $G=Gal(L/\Bbb{Q})$ acts transitively on the set of ten roots. I haven't checked all the details, but it seems to me that $G$ has a subgroup $H=Gal(L/K)$ of index two that acts as the dihedral group on the two pentagons. And then the elements in $G\setminus H$ interchange the two pentagons.

Jyrki Lahtonen
  • 133,153