I have this Fresnel integral:
$$C(x)=\int_0^x \cos\!\big(t^2\big)\,dt$$
And Maclaurin Series for it is:
$\sum_{n=0}^\infty (-1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}$
The question is how to choose a proper amount of elements in series required for correct function approximation between $[0 \le x \le3]$ (for example)
There is no proper number of elements unless you specify an accuracy criterion. The series converges for all $x$. When $x\gt 0$ the series is eventually alternating in sign, so you can use the alternating series theorem. Add up enough terms until the terms start decreasing, then the truncation error will be smaller than the first neglected term. When you get to a term less than your error bound, add it in. The remaining error will be of opposite sign to the last term added and smaller in absolute value.
As an example, say $x=2$. The terms are shown below. If you require accuracy to $10^{-6}$ you would evaluate the series up to $n=9$, notice that term is less than $10^{-6}$ in absolute value, and declare victory. As $x$ gets large it will take more and more terms. You might then want to use some other approximation.
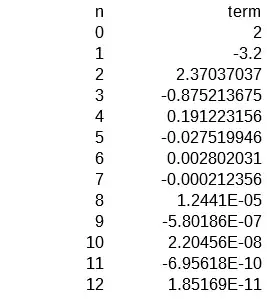
You want to solve for $n$ $$\frac{x^{4n+1}}{(4n+1)(2n)!}\leq \epsilon \tag 1$$ The lhs can be approximated by $$\frac{x^{4n+1}}{(4n+1)(2n)!}\sim\frac{x^{4n+1}}{2(2n+1)(2n)!}=\frac 1{2x} \frac {(x^2)^{2n+1}}{(2n+1)!}$$ So, we need to solve for $n$ $$(2n+1)!=\frac {(x^2)^{2n+1}}{2x\epsilon}$$ For the time being, let $m=2n+1$, $x^2=a$ and $2x \epsilon=10^{-k}$ to make $$m!=a^m 10^k$$ If you look at this question of mine, you will see a magnificent approximation built by @robjohn for this last equation. $$ m\sim ea\exp\left(\operatorname{W}\left(\frac k{ea}\log(10)-\frac1{2ea}\log(2\pi a)\right)\right)-\frac12$$ where appears Lambert function.
Applied to your case, this would give
$$2n+1=e x^2\exp\left(W\left(-\frac{\log \left(8 \pi x^4 \epsilon ^2\right)}{2 e x^2}\right)\right)-\frac12\tag 2$$
Now, let $\epsilon=10^{-p}$ and $x=2$ as Ross Millikan used for the test and you will get for $n$ the approximation given by $(2)$ as well as the exact solution of $(1)$ $$\left( \begin{array}{ccc} p & \text{approximation} & \text{solution} \\ 1 & 4.32647 & 4.32867 \\ 2 & 5.44001 & 5.44150 \\ 3 & 6.39673 & 6.39788 \\ 4 & 7.26127 & 7.26220 \\ 5 & 8.06292 & 8.06372 \\ 6 & 8.81800 & 8.81869 \\ 7 & 9.53669 & 9.53731 \\ 8 & 10.2259 & 10.2264 \\ 9 & 10.8905 & 10.8910 \\ 10 & 11.5342 & 11.5347 \\ 11 & 12.1599 & 12.1603 \\ 12 & 12.7696 & 12.7700 \end{array} \right)$$
and you need to use $\lceil n \rceil$.
Edit
The results are quite sensitive to the value of $x$. Using $x=3$, we should get for $n$ $$\left( \begin{array}{ccc} p & \text{approximation} & \text{solution} \\ 1 & 10.7036 & 10.7166 \\ 2 & 11.8740 & 11.8847 \\ 3 & 12.9471 & 12.9562 \\ 4 & 13.9492 & 13.9572 \\ 5 & 14.8966 & 14.9037 \\ 6 & 15.7999 & 15.8063 \\ 7 & 16.6668 & 16.6727 \\ 8 & 17.5029 & 17.5083 \\ 9 & 18.3125 & 18.3175 \\ 10 & 19.0989 & 19.1036 \\ 11 & 19.8648 & 19.8692 \\ 12 & 20.6125 & 20.6166 \end{array} \right)$$
