Edited answer...
which starts with a comment.
The title Looking for the best way to find Pythagorean triples where $B−A=\pm1$ is possibly misleading for the actual question, which after many comments can be extracted only from the fact that the initial answer for the $(A,C)$ recursion (remained in the sequel) is not the wanted answer. Please always make clear in the OP which is the question (without alternatives, best stated as question, not as a wish).
The OP gives two ways to construct Pythagorean triples, one is "from a book" and constructs triples $T_x=(A_x,B_x,C_x)$ recursively, the other one comes from a formula, it constructs intermediate pairs $P_x=(m_x,n_x)$ given by an other recursion, that may be used to reconstruct $(A_x,B_x,C_x)$. As i extract the information from the comments, we need only the $P_x$ (despite of the title, and the initial digression / divagation on triples). OK, this is even simpler.
We have the linear recursion formula for the pair written as column vector
$$
\begin{aligned}
\begin{bmatrix}
m_{x+1}\\
n_{x+1}
\end{bmatrix}
&=
\begin{bmatrix}
2&1\\1&0
\end{bmatrix}
\begin{bmatrix}
m_{x}\\
n_{x}
\end{bmatrix}
\\
&=
\underbrace{
\begin{bmatrix}
1+\sqrt 2&1-\sqrt 2\\1&1
\end{bmatrix}}_C
\underbrace{
\begin{bmatrix}
1+\sqrt 2&\\&1-\sqrt 2
\end{bmatrix}}_D
\underbrace{
\frac 1{2\sqrt 2}
\begin{bmatrix}
1 &\sqrt 2-1\\-1&\sqrt 2+1
\end{bmatrix}}_{C^{-1}}
\begin{bmatrix}
m_{x}\\
n_{x}
\end{bmatrix}
\ ,
\end{aligned}
$$
with a diagonal matrix $D$ above. The powers of
$\begin{bmatrix}2&1\\1&0\end{bmatrix}$ are not immediate, but the powers of $D$ are.
We get directly for your pairs formula the explicit version with proof:
$$
\begin{aligned}
\begin{bmatrix}
m_x\\n_x
\end{bmatrix}
&=
(CDC^{-1})^x\begin{bmatrix}m_0\\n_0\end{bmatrix}
=
CD^xC^{-1}\begin{bmatrix}1\\0\end{bmatrix}
\\[2mm]
&=
\frac 1{2\sqrt 2}
\begin{bmatrix}
1+\sqrt 2&1-\sqrt 2\\1&1
\end{bmatrix}
\begin{bmatrix}
(1+\sqrt 2)^x&\\&(1-\sqrt 2)^x
\end{bmatrix}
\begin{bmatrix}
1 &\sqrt 2-1\\-1&\sqrt 2+1
\end{bmatrix}
\begin{bmatrix}1\\0
\end{bmatrix}
\\[2mm]
&=
\frac 1{2\sqrt 2}
\begin{bmatrix}
(1+\sqrt 2)^{x+1} & (1-\sqrt 2)^{x+1}\\
(1+\sqrt 2)^{x } & (1-\sqrt 2)^{x }
\end{bmatrix}
\begin{bmatrix}
1 &\sqrt 2-1\\-1&\sqrt 2+1
\end{bmatrix}
\begin{bmatrix}1\\0
\end{bmatrix}
\\[2mm]
&=
\frac 1{2\sqrt 2}
\begin{bmatrix}
(1+\sqrt 2)^{x+1} - (1-\sqrt 2)^{x+1} & ? \\
(1+\sqrt 2)^{x } - (1-\sqrt 2)^{x } & ?
\end{bmatrix}
\begin{bmatrix}1\\0
\end{bmatrix}
\\[2mm]
&=
\frac 1{2\sqrt 2}
\begin{bmatrix}
(1+\sqrt 2)^{x+1} - (1-\sqrt 2)^{x+1} \\
(1+\sqrt 2)^{x } - (1-\sqrt 2)^{x }
\end{bmatrix}
\ ,
\end{aligned}
$$
which gives $\displaystyle n_x=\frac 1{2\sqrt 2}\Big(\ (1+\sqrt 2)^{x } - (1-\sqrt 2)^{x }\ \Big)$.
$\square$
In particular, for $x>0$ we can compute $n_x$ by rounding to an integer the number $\displaystyle n_x=\frac 1{2\sqrt 2} (1+\sqrt 2)^x$. For instance, for $x=7$ we obtain $168.99926035179\dots$ and after rounding we get $n_7=169$.
Older answer for the explicit form of the $(A,C)$ recursion:
You may try to write explicitly the recursion formula as passing from one pair $(A,C)$ to the next pair $(A',C')$ in the form:
$$
\begin{aligned}
\begin{bmatrix}
A'\\C'\\1
\end{bmatrix}
&=
\underbrace{
\begin{bmatrix}
3&2&1\\4&3&2\\0&0&1
\end{bmatrix}}_{=:T}
\begin{bmatrix}
A\\C\\1
\end{bmatrix}
\ ,
\\
&\qquad\text{ extracted from the mentioned passage}
\\
A' &=3A+2C+1\ ,\\
C' &=4A+3C+2\ ,
\end{aligned}
$$
thus introducing a matrix $T$. Its charactristic polynomial is $(x - 1) (x^2 - 6x + 1)$, so we have the following diagonalization over $\Bbb Q(a)$ with $a=\sqrt 2$. We expect a diagonal matrix with diagonal entries corresponding to the roots of the above characteristic polynomial, they are $1$ and $3\pm 2\sqrt 2$. Computer aided typing:
sage: K.<a> = QuadraticField(2)
sage: a^2
2
sage: T = matrix( K, 3,3, [3,2,1, 4,3,2, 0,0,1] )
sage: T
[3 2 1]
[4 3 2]
[0 0 1]
sage: D, change = T.jordan_form(transformation=True)
sage: D
[ 2*a + 3| 0| 0]
[--------+--------+--------]
[ 0| 1| 0]
[--------+--------+--------]
[ 0| 0|-2*a + 3]
sage: change
[ 1 1 1]
[ a 0 -a]
[ 0 -2 0]
sage: change * D * change^-1 == T
True
Later edit: Let us use, and type explicitly the obtained formula for $T$, and thus also for the powers of $T$. Below, $S$ is the base change matrix.
$$
\begin{aligned}
T
&=
\underbrace{
\begin{bmatrix}
1&1&1\\
a&0&-a\\
0&-2&0
\end{bmatrix}}_S
\begin{bmatrix}
3+2a&&\\
&1&\\
&&3-2a
\end{bmatrix}
\underbrace{
\frac 14
\begin{bmatrix}
2 & a & 1\\
0&0&-2\\
2&-a&1
\end{bmatrix}}_{S^{-1}}
\\
T^n
&=
\frac 14
\begin{bmatrix}
1&1&1\\
a&0&-a\\
0&-2&0
\end{bmatrix}
\begin{bmatrix}
(3+2a)^n&&\\
&1&\\
&&(3-2a)^n
\end{bmatrix}
\begin{bmatrix}
2 & a & 1\\
0&0&-2\\
2&-a&1
\end{bmatrix}
\\[3mm]
&\qquad\text{ Above }a=\sqrt 2\ .
\\
&\qquad\text{ This gives an }\color{blue}{\text{explicit formula}:}
\\[3mm]
\color{blue}{
\begin{bmatrix}
A_n\\ C_n\\ 1
\end{bmatrix}}
&=
T^n
\begin{bmatrix}
A_0\\ C_0\\ 1
\end{bmatrix}
=
T^n
\begin{bmatrix}
0\\ 1\\ 1
\end{bmatrix}
\\
&=
\color{blue}{
\frac 14
\begin{bmatrix}
1&1&1\\
a&0&-a\\
0&-2&0
\end{bmatrix}
\begin{bmatrix}
(3+2a)^n&&\\
&1&\\
&&(3-2a)^n
\end{bmatrix}
\begin{bmatrix}
2 & a & 1\\
0&0&-2\\
2&-a&1
\end{bmatrix}
\begin{bmatrix}
0\\ 1\\ 1
\end{bmatrix}}\ .
\end{aligned}
$$
$\square$
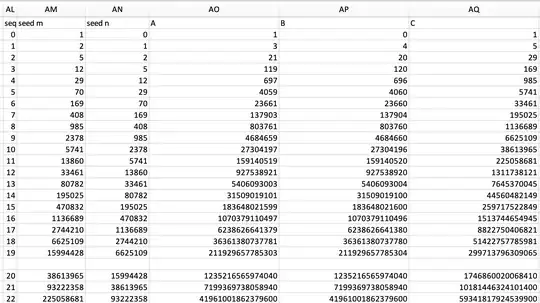
Please stop reading here if computer experiments are not welcome. (I posted this since the shape of the OP also has similar collection of data. It is often for me a check, and in this case it may be helpful for some readers, too.)
Example of an explicit computation:
To compute -say- the $15$.th term (or so) we already have $D^{15}$, so compute with sage the product:
$$
\frac 14
\begin{bmatrix}
1&1&1\\
a&0&-a\\
0&-2&0
\end{bmatrix}
\begin{bmatrix}
(3+2a)^{15}&&\\
&1&\\
&&(3-2a)^{15}
\end{bmatrix}
\begin{bmatrix}
2 & a & 1\\
0&0&-2\\
2&-a&1
\end{bmatrix}
\begin{bmatrix}
0\\1\\1
\end{bmatrix}
\ ,
$$
and we get:
sage: Z = matrix(3, 1, [0,1,1]) # initial solution, A=0, C=1
sage: change * D^15 * change^-1 * Z
[183648021599]
[259717522849]
[ 1]
sage: A15, C15 = 183648021599, 259717522849
sage: B15 = A15 + 1
sage: A15^2 + B15^2 == C15^2
True
This is the kind of direct computation needed. (The diagonal matrix $D$ has diagonal entries $1$, and $3\pm 2\sqrt 2$, so the only involved involved computation is the one of the powers of these diagonal entries.)