I am no graph-theory expert, but I've been thinking about this problem for a long time.
Let $G_n$ be the $n$-dimensional, infinite, unit-square-grid graph, i.e. the graph whose vertices are the points of $\mathbb{Z}^n$ and that has one edge between each couple of vertices separated by a Euclidean distance of 1.
I know that, for any $d$ in $\mathbb{N}$, the set $\mathbb{Z}^d$ is countably infinite, i.e. one can find a bijection between $\mathbb{N}$ and $\mathbb{Z}^d$. That is not the issue here.
My question is: what are the conditions under which that graph contains a Hamiltonian ray? In other words, under what conditions does a path starting at some vertex of the graph and visiting each vertex of $G_n$ exactly once (by jumping from one vertex to an adjacent vertex) exists?
Because of invariance of $G$ by translation by any basis unit vector, we can consider, without loss of generality, that such a ray starts at the origin.
It's easy to see that:
- in the $n=1$ case, no such ray exists: whichever direction you set off on the number line, you can not doubleback to collect the integers located on the other side from the origin;
- in the $n=2$ case, there is an infinite number of such rays: an easy example is some "square spiral" starting from the origin.
However, the answer for $n\geq3$ eludes me.
As an attempt to solve the $n=3$ case, I set out to answer a related question: whether the subgraph (let's call it $G_3'$) of $G_3$ whose coordinates are in $\{-1,0,1\}^3$ contains a Hamiltonian ray starting at the origin. Not knowing any better, I settled the issue by brute force in Matlab (see the code below, in which you can change the starting point).
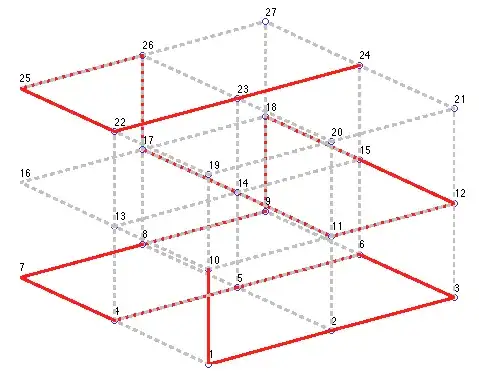
Result: $G_3'$ does not contain a Hamiltonian ray starting at the origin.
My intuition leads me to conjecture that such a path exists in $G_n$ if and only if $n$ is even.
What do YOU think? Is a result known?
Matlab script:
tic
%clc
a=0.7;
% ---------------- vertex generation ------------------
N=3; % number of nodes along one edge
% generation of the coordinate vectors x, y, z
for k=1:3
temp=[];
for m=0:N-1
temp=[temp m*ones(1,N^(k-1))];
end
temp2=[];
for n=1:N^(3-k)
temp2=[temp2 temp];
end
switch k
case 1
x=temp2;
case 2
y=temp2;
case 3
z=temp2;
end
end
% ------------------ plotting and labelling the vertices -----------
fig = figure;
set(fig,'color',[1 1 1]);
ax = axes;
plot3(x,y,z,'o');
axis off
for k=1:N^3
text(x(k),y(k),z(k)+0.1,num2str([N^0 N^1 N^2] * [x(k) y(k) z(k)]'+1));
end
% ----------------- generating the edges and the adjacency matrix ------------------
edge_h = zeros(53,1);
edges = zeros(53,1);
% adjacency matrix
A=zeros(N^3,N^3);
n=0;
for i=1:N^3
vi = [N^0 N^1 N^2] * [x(i) y(i) z(i)]';
for j=1:N^3
vj = [N^0 N^1 N^2] * [x(j) y(j) z(j)]';
weight = sum(([x(j) y(j) z(j)]-[x(i) y(i) z(i)]).^2);
if (weight == 1) && isempty(find(edges(:,1) == vj + sqrt(-1)*vi)) % (vi,vj) is an edge
% update adjacency matrix
A(i,j)=1;
A(j,i)=1;
edge_h(n+1)=line([x(i) x(j)],[y(i) y(j)],[z(i) z(j)],'Color',a*[1 1 1],...
'Linestyle',':',...
'LineWidth', 2);
vi = [N^0 N^1 N^2] * [x(i) y(i) z(i)]';
vj = [N^0 N^1 N^2] * [x(j) y(j) z(j)]';
edges(n+1,1) = vi+sqrt(-1)*vj;
n = n + 1;
%pause(0.1)
end
end
end
toc
% ------- look for a Hamiltonian path starting by the given path -------
%path_init = [14 5 2]; % starting point
path_init = 10;%[2 1]; %[2 11]
path = path_init;
flag=0;
chemin=line(x(path),y(path),z(path),'Color',a*[1 1 1],'Linestyle',':','LineWidth', 2);
while numel(path)<N^3
[ path , flag ]=recursive_path_finding( path ,flag , A );
delete(chemin)
chemin=line(x(path),y(path),z(path),'Color',[1 0 0],'Linestyle','-','LineWidth', 2);
drawnow
%pause(0.1)
if numel(path) == numel(path_init)
disp('No Hamiltonian path for which the initial path considered is a subgraph.');
break
end
end
set(fig,'Name',['Path length: ' num2str(path)]);
recursive_path_finding.m function:
function [ path1 , flag1 ]=recursive_path_finding( path0 , flag0 , A )
% NOTE: neighb(i) informs on the order of path0(i+1) as a neighbour of path0(i)
switch flag0
case 0 % path0(end) has just been added to path0. Find a neighbour of path0(end) that hasn't already been explored.
u = find(A(path0(end),:)==1); % Find all the neighbours of path0(end).
for k=1:length(u)
% Check that u(k) has not already been explored.
temp = find(path0==u(k));
if isempty( temp ) % Not yet explored: add it to the path and break the loop.
path1 = [path0 u(k)];
flag1 = 0;
break % A new candidate for the next step has been found, not need to carry on the loop interations.
end
end
if ~exist('path1') % All the neighbours of path(end) have been explored, so path0(end) is not a valid candidate. Backtrack.
path1 = path0;
flag1 = path0(end);
end
otherwise % path0(end) is not a valid candidate.
u = find(A(path0(end-1),:)==1); % Find all the neighbours of path0(end-1).
v = u(find(u>flag0)); % Discard all the neighbours of path0(end-1) listed before flag0 (inclusive).
for k = 1 : length(v) % Test all the neighbours of path0(end-1) listed AFTER the (previously tested) flag0.
% Check that v(k) has not already been explored.
temp = find(path0==v(k));
if isempty( temp ) % Not yet explored: add it to the path and break the loop.
path1 = [path0(1:end-1) v(k)];
flag1 = 0;
break % A new candidate has been found in place of path0(end), not need to carry on the loop interations.
end
end
if ~exist('path1') % All the neighbours of path(end-1) have been explored, so path0(end-1) is not a valid candidate. Backtrack.
path1 = path0(1:end-1);
flag1 = path0(end-1);
end
end