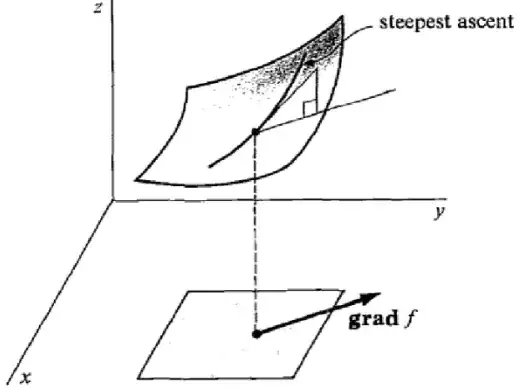
The direction of the gradient vector.

Question

The direction of the gradient is along the direction of the maximum ascent, or along the directional derivative that has by the most positive value, but when talking about level surfaces, it is agued that gradient is always perpendicular to the tangent plane? This is confusing me a lot? Have I not clearly understood the difference between a level surface and a plot of a two dimensional function? Is there any difference at all?

Answer 1

For a function $z=f(x,y)$ both the level lines and the gradient vector belong to the $(x,y)$ plane and the gradient vector is othogonal to them.

(credits)

For a function $w=f(x,y,z)$, the level surfaces and the gradient vectors belong to the space $\mathbb R^3$.

Answer 2

You seem to be confused as to how the gradient can point in the direction of maximum ascent and be perpendicular to a level curve at the same time. Perhaps this will make more sense if we use our imagination some.

Given $z=f(x,y)$, note that the gradient of $f$, or $<f_x, f_y>$, is a vector in the $xy$-plane. Let $P_1(x_1, y_1, z_1)$ be some arbitrary point on the $3$D surface given by $f$. As you stand there on the surface at $P_1$, you can imagine the gradient as a vector that's parallel to the $xy$-plane pointing in the direction you must move in order to experience the maximum rate of change. If we hold $z$ constant at $z_1$, we get a level curve that passes through the point where we are standing. Note that this level curve is also parallel to the $xy$-plane. So both the gradient and level curve are parallel to the $xy$-plane. We will find that the gradient is perpendicular to the level curve at the point where we are standing, and the gradient still points in the direction of maximum ascent with respect to the $3$D surface.