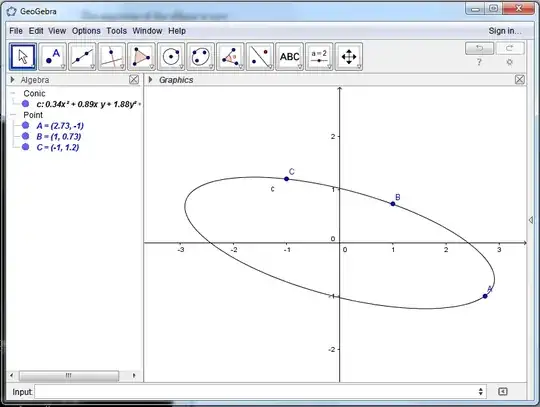
How to draw an ellipse if a center and 3 arbitrary points on it are given?

Question

How to draw an ellipse if a center and 3 arbitrary points on it are given?

Answer 1

The generally centered 2D ellipse equation is

$$ \begin{pmatrix} x\\y\\1 \end{pmatrix}^\top \begin{bmatrix} C_{11} & C_{12} & 0 \\ C_{12} & C_{22} & 0 \\ 0 & 0 & -1 \end{bmatrix} \begin{pmatrix} x\\y\\1 \end{pmatrix} = 0 \\ C_{11} x^2 + C_{22} y^2 + 2 C_{12} x y - 1 = 0$$

Using the three points you can find the three coefficients $C_{11}$, $C_{22}$ and $C_{12}$. First form a 3×3 system using the above equation for the three points $(x_1,y_1)$, $(x_2,y_2)$ and $(x_3,y_3)$.

$$\begin{bmatrix} x_1^2 & y_1^2 & 2 x_1 y_1 \\x_2^2 & y_2^2 & 2 x_2 y_2 \\ x_3^2 & y_3^2 & 2 x_3 y_3 \end{bmatrix} \begin{pmatrix} C_{11} \\ C_{22} \\ C_{12} \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}$$

The above system is easily solved by inverting the 3×3 matrix, resulting in:

$$\begin{array}{ccl} C_{11} & = & \frac{y_2^2 2 x_3 y_3 - 2 x_2 y_2 y_3^2 + 2 x_1 y_1 y_3^2 - y_1^2 2 x_3 y_3 + y_1^2 2 x_2 y_2 - 2 x_1 y_1 y_2^2}{|M|} \\ C_{22} & = & \frac{2 x_2 y_2 x_3^2 - x_2^2 2 x_3 y_3 + x_1^2 2 x_3 y_3 - 2 x_1 y_1 x_3^2 + 2 x_1 y_1 x_2^2 - x_1^2 2 x_2 y_2}{|M|} \\ C_{12} & = & \frac{x_2^2 y_3^2 - y_2^2 x_3^2 + y_1^2 x_3^2 - x_1^2 y_3^2 + x_1^2 y_2^2 - y_1^2 x_2^2}{|M|} \end{array} $$

where the determinant $|M|$ is:

$$ |M| = x_1^2 (y_2^2 2 x_3 y_3 - 2 x_2 y_2 y_3^2) + y_1^2 (2 x_2 y_2 x_3^2 - x_2^2 2 x_3 y_3) + 2 x_1 y_1 (x_2^2 y_3^2 - y_2^2 x_3^2) $$

Once the coefficients are known you can find the angle of incline of the ellipse by $$ \theta = \frac{1}{2} \arctan \left( \frac{2 C_{12}}{C_{22}-C_{11}} \right) $$

_{Note the angle is measured clockwise from horizontal}

Getting the semi-major and semi-minor axes $a$ and $b$ is a little more involved.

• Find $\eta = C_{11} + C_{22}$
• Find $\zeta = \frac{C_{22}-C_{11}}{\cos(2 \theta)}$
• Semi major axis $a= \sqrt{ \frac{2}{\eta - \zeta} }$
• Semi minor axis $b= \sqrt{ \frac{2}{\eta + \zeta} }$

The equation of the ellipse can now alternatively be expressed in terms of $\theta$, $a$, and $b$:

$$ \left( \frac{(b^2-a^2) \cos^2 \theta}{a^2 b^2} + \frac{1}{b^2} \right) x^2 + \left( \frac{(a^2-b^2)\cos^2\theta}{a^2 b^2} + \frac{1}{a^2} \right) y^2 + \frac{2 (a^2 - b^2)\sin\theta\cos\theta}{a^2 b^2} x y - 1 = 0$$

Example

Consider the points $(\sqrt{3}+1,-1)$, $(1,\sqrt{3}-1)$ and $(-1,\frac{5 \sqrt{3}}{13} + \frac{7}{13})$

Find the coefficients $$\begin{pmatrix} C_{11} \\ C_{22} \\ C_{12} \end{pmatrix} = \begin{pmatrix} \frac{5-2\sqrt{3}}{9} \\ \frac{2 \sqrt{3}+5}{9} \\ \frac{2}{9} \end{pmatrix} $$

Find the angle $$\theta = \frac{1}{2} \arctan \left( \frac{1}{\sqrt{3}} \right) = \frac{\pi}{12}$$

Find the axes:

• $\eta = \frac{10}{9}$
• $\zeta = \frac{8}{9}$
• $a^2 = \frac{2}{\frac{2}{9}}= 9$
• $b^2 = \frac{2}{2} = 1$

Find the ellipse equation

$$ \left( \frac{5}{9} - \frac{2 \sqrt{3}}{9} \right) x^2 + \left( \frac{2 \sqrt{3}}{9} + \frac{5}{9} \right) + \frac{4}{9} x y - 1 =0 $$

Confirm results with GeoGebra:

Answer 2

If a center point $C$ is chosen for the ellipse, one can draw two intersecting ellipses with center at $C$ which intersect at four points. So if $A,B$ happen to be two of those four points, the ellipse will not be unique. So I think you might need more assumptions, maybe that the ellipse is to have its major axis parallel to the $x$ axis.

Just saw the update: The above example shows you need at least 5 points given on the ellipse to determine it.

ADDED: Consider the following two ellipses, both centered at $(0,0)$. $$E_1:\ x^2+2y^2=3,\\ E_2:\ 2x^2+y^2=3.$$ The four points $$(1,1),\ (1,-1),\ (-1,1),\ (-1,-1)$$ each lie on both ellipses $E_1$ and $E_2$. So in general given only four points and the center, the ellipse is not determined.

Answer 3

The center $C$ is given, and three points $P_1, P_2, P_3$ are also given.

The equation of an ellipse centered at $C$ is given by

$ (r - C)^T Q (r - C) = 1 \hspace{25pt}(1) $

where $r= [x, y]^T$ and $Q$ is a symmetric $2 \times 2 $ matrix

$ Q = \begin{bmatrix} Q_{11} && Q_{12} \\ Q_{12} && Q_{22} \end{bmatrix} \hspace{25pt} (2) $

Substituting the given three points and $C$ into (1), we get a linear system in $Q_{11}, Q_{12}, Q_{22} $, namely,

if $C = [x_0, y_0]^T $ and $P_1 = [x_1, y_1]^T , P_2 = [x_2, y_2]^T, P_3 = [x_3, y_3]^T $, then the linear system is

$ Q_{11} (x_1 - x_0)^2 + 2 Q_{12} (x_1 - x_0)(y_1 - y_0) + Q_{22} (y_1 - y_0)^2 = 1 $

$ Q_{11} (x_2 - x_0)^2 + 2 Q_{12} (x_2 - x_0)(y_2 - y_0) + Q_{22} (y_2 - y_0)^2 = 1 $

$ Q_{11} (x_3 - x_0)^2 + 2 Q_{12} (x_3 - x_0)(y_3 - y_0) + Q_{22} (y_3 - y_0)^2 = 1 $

And this can be solved easily for $Q_{11}, Q_{12}, Q_{22}$. At this point we must note that the three points cannot any three points. For the above linear system to be solvable uniquely, any two of the three points cannot be symmetric about the center $C$, because in this case we will have only two independent equations in the three unknowns.

Once $Q_{11}, Q_{12}, Q_{13}$ have been computed, then the algebraic equation of the ellipse is fully specified.

To actually draw the ellipse required that you diagonalize the symmetric matrix $Q$, i.e. write $Q$ as follows

$$ Q = R D R^T $$

where $D$ is diagonal and $R$ is orthogonal. This is done as follows

Step 1: Compute the angle $\theta$ using

$ \theta = \dfrac{1}{2} \tan^{-1} \left( \dfrac{2 Q_{12} }{Q_{11} - Q_{22} } \right) $

Then immediately, you get the matrix $R$ which is given by

$ R = \begin{bmatrix} \cos \theta && - \sin \theta \\ \sin \theta && \cos \theta \end{bmatrix} $

The diagonal elements of the diagonal matrix $D$ are computed as follows

$ D_{11} = Q_{11} \cos^2 \theta + Q_{22} \sin \theta + 2 Q_{12} \sin(\theta) \cos(\theta) $

$ D_{22} = Q_{11} \sin^2 \theta + Q_{22} \cos \theta - 2 Q_{12} \sin(\theta) \cos(\theta) $

Now, we're ready to plot the ellipse. Remember that

$ (r - C)^T Q (r - C) = 1 $

Plugging in $ Q = R D R^T $ into the above equation gives us

$ (r - C)^T R D R^T (r - C) = 1 $

Now define vector $z = D^{(1/2)} R^T (r - C) $

Then

$ z^T z = 1 $

That is, $z$ is a unit vector. Any unit vector in $\mathbb{R}^2 $ can be written as follows

$ z = \begin{bmatrix} \cos(t) \\ \sin(t) \end{bmatrix} $

Hence, from the above relation between $z$ and $r$, we get

$r = C + R D^{-(1/2)} z $

So all we need to generate all the points of the ellipse is compute the matrix $A = {R D}^{-(1/2)} $, then we have

$ r = \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} C_x + A_{11} \cos(t) + A_{12} \sin(t) \\ C_y + A_{21} \cos(t) + A_{22} \sin(t) \end{bmatrix} $

Answer 4

Actually I was suggesting my above answer to the people at geogabra and they told me about this nice parametric equation that only needs the center point and any 2 points on the ellipse, where A is the center: f(t)=A+(B-A)*sin(t)+(C-A)*cos(t)

Answer 5

You must find three unknowns - two half axes describing the ellipse and an angle to describe it's orientation.

You must choose some equation that describes ellipse and write the equations for each of the points. Find the parameters of ellipse from them.

For example, with parametric equations you have two equations at each point: $$x_i=x_c+a\cos t_i \cos \varphi - b \sin t_i \sin \varphi$$ $$y_i=y_c+a\cos t_i \sin \varphi - b \sin t_i \cos \varphi$$

where $x_i$ and $y_i$ are the coordinates of $i$-th point, $x_c$ and $y_c$ are the centers coordinates, $t_i$ is parameters $t$ value at the $i$-th point and $a$, $b$ and $\varphi$ are the unknown values describing the ellipse and it's orientation. If you write these equations, you will have six equations and six unknown values (three $t_i$'s and the wanted values). Solvable, but not trivial. I'm showing you the approach not the solution. I'll leave it up to you to choose more appropriate ellipse equations to start with :)

Answer 6

Suppose the center is the vector $C$ and the three points through which the ellipse passes are $P_1, P_2, P_3$ then a parametric equation of this ellipse is

$ P(t) = C + F_1 \cos(t) + F_2 \sin(t) $

where $F_1$ and $F_2$ are called the conjugate semi-diameters, and are not unique. So now define

$V_1 = P_1 - C , V_2 = P_2 - C , P_3 - C $ then

Then the shifted ellipse has the equation

$ V(t) = F_1 \cos(t) + F_2 \sin(t) $

We can choose $V(0) = F_1 $ to be $V_1$ , then

$ V(t) = V_1 \cos(t) + F_2 \sin(t) $

At times $t_1$ and $t_2$ we have

$ V(t_1) = V_2 = V_1 \cos(t_1) + F_2 \sin(t_1) $

Now, since we are in $2D$, then $V_3 = c_1 V_1 + c_2 V_2$, and $F_2 = a V_1 + b V_2 $ where $c_1$ and $c_2$ are known, while $a$ and $b$ are unknown.

With this, and from the linear independence of $V_1$ and $V_2$ , it follows that

$ 0 = \cos(t_1) + a \sin(t_1) \hspace{15pt}(1)$

$ 1 = b \sin(t_1) \hspace{15pt}(2)$

And finally, at $t = t_2$ we have

$ V(t_2) = V_3 = c_1 V_1 + c_2 V_2 = V_1 \cos(t_2)+ (a V_1 + b V_2) \sin(t_2) $

From which we get another two equations

$ c_1 = \cos(t_2) + a \sin(t_2) \hspace{15pt}(3) $

$ c_2 = b \sin(t_2) \hspace{15pt}(4)$

Eliminating $a$ and $b$ from equations $(1)-(4)$ yields the following system of two equations in $t_1 $ and $t_2 $:

$$\sin(t_1 - t_2) = c_1 \sin(t_1)$$ $$\sin(t_2) = c_2 \sin(t_1)$$

It was shown here that the solution to this system of equations is given by

$$ cos(t_1) = \dfrac{1 - c_1^2 - c_2^2}{2 c_1 c_2} \\ cos(t_2 ) = \dfrac{1 + c_1^2 - c_2^2}{2 c_1}$$

Using the first of these equations, we get the value of $t_1$, and then using equations $(1)$ and $(2)$ we get:

$$ a = - \cot(t_1), \ b = \dfrac{1}{\sin(t_1) } $$

Thus, we have determined vector $F_2 = a V_1 + b V_2 $, and therefore the parametric equation of the ellipse is now fully specified, and can be used explicitly to find the ellipse points $P(t)$ at any value of the parameter $t \in [0, 2\pi)$

And finally, if the algebraic equation of the ellipse is required, then, it is quite easy to show that it is given by

$ (r - C)^T Q ( r - C) = 1 $

where $ Q = F^{-T} F^{-1} $ and $F = \begin{bmatrix}F_1 && F_2 \end{bmatrix} $

Answer 7

I think I found an answer, you don't need to know the center but you have to know which 3 points on the diagram you know, I called it the

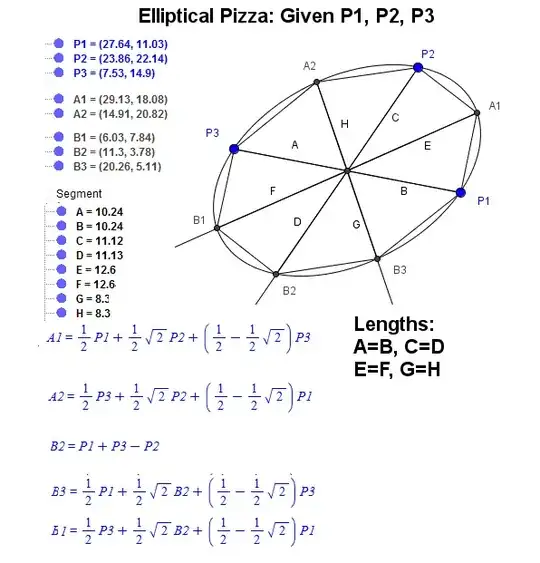
, once you find 2 additional points using the formulas you find the conic through 5 points as here Conic through 5 points...

I posted it on my blog here: Elliptical Pizza on Ben Paul Thurston Blog