0

If X is a continuous random variable which takes non-negative value, prove that the expectation of X can be calculated using the following integral:

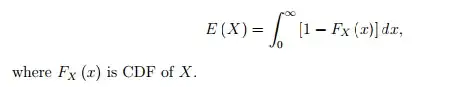
enter image description here

mathaholic
  • 301
  • You may use the definition of $E(X)$ and try integration by parts. – Berkheimer Mar 23 '13 at 15:43
  • You might want to stop posting your homework here without any clue whatsoever on what you tried, why this failed, and what in the exercise is causing you trouble. – Did Mar 23 '13 at 17:05
  • The result in question is not restricted to continuous random variables but holds for other random variables as well. For informal explanations as to why it is true in the case of discrete random variables as well as a formal proof for the general case, see the answers to this question. – Dilip Sarwate Mar 25 '13 at 03:53

1 Answers1

2

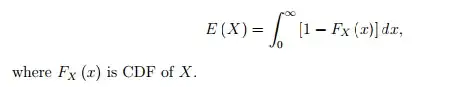
Write $x = \int_{[0,x)} 1\,dt$, so that $$ \eqalign{ E(X) &=E\left(\int_{[0,X)} 1\,dt\right) =E\left(\int_0^\infty{\Bbb 1}_{\{X>t\}} \,dt\right)\cr &= \int_0^\infty P(X>t) \,dt=\int_0^\infty [1-F_X(t)]\,dt.\cr } $$ (The third equality results from the Fubini/Tonelli theorem.) This argument works for any non-negative random variable, continuous or not.

John Dawkins
  • 221