3

I tried for a few days to prove the identity $\sin(x)\cos(x)=\frac{\sin(2x)}{2}$ and finally got the following proof. I wanted to know if someone knew a simpler or more elegant way to proof it.

enter image description here

$$\begin{align}\dfrac{\cos(\phi)}{\frac{1+\cos(2\phi)}{2}}&=\dfrac{1}{\sqrt{\frac{(1+\cos(2\phi))²+\sin²(2\phi)}{4}}} ~~~~~~~~~~~~~~~*\frac{1+\cos(2\phi)}{2}\\ \cos(\phi) &=\dfrac{\frac{1+\cos(2\phi)}{2}}{\sqrt{\frac{1+2 \cos(2\phi)+ \cos²(2\phi)+sin²(2\phi)}{4}}}\\ \cos(\phi)&=\dfrac{\frac{1+\cos(2\phi)}{2}}{\sqrt{\frac{1+\cos(2\phi)}{2}}}\\ \cos(\phi)&=\sqrt{\frac{1+\cos(2\phi)}{2}}\\ \cos²(\phi)&=\frac{1+\cos(2\phi)}{2}\end{align}$$

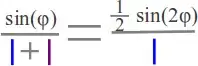
enter image description here

$\begin{align}\frac{\sin(\phi)}{\cos(\phi)}&=\dfrac{\frac{\sin(2\phi)}{2}}{\frac{1+\cos(2\phi)}{2}}\\ \frac{\sin(\phi)}{\cos(\phi)}&=\dfrac{\frac{\sin(2\phi)}{2}}{\cos²(\phi)}\\ \sin(\phi)\cos(\phi)&=\frac{\sin(2\phi)}{2}\end{align}$

I also tried this: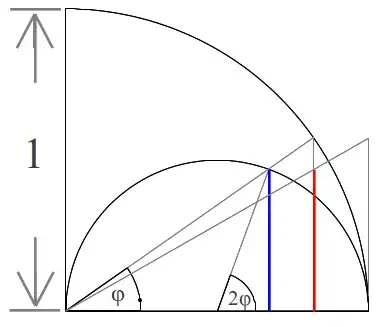
enter image description here
showing that 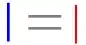enter image description here but didn't manage. I would be glad if someone had an idea on this.

Michael Hardy
  • 1
whateverguy
  • 123
  • Here's my picture-proof of the angle sum (and difference) identities: http://math.stackexchange.com/a/1342/409 . Set $\alpha = \beta$ for your question. – Blue Mar 23 '13 at 03:08
  • Prove is the verb, and proof is the noun! – Pedro Mar 23 '13 at 04:19

5 Answers5

3

It is a nice argument. Alternately, at least for $0\lt 2\varphi\lt \pi$, let $ABC$ be a triangle, with $AB=AC=1$ and $\angle CAB=2\varphi$.

Drop a perpendicular from $A$ to $BC$, meeting $BC$ at $M$. Note that $AM=\cos\varphi$ and $BM=\sin\varphi$. So $BC=2\sin\varphi$, and therefore the area of $\triangle ABC$ is $\cos\varphi\sin\varphi$.

But the area of $\triangle ABC$ is $\frac{1}{2}\sin 2\varphi$.

Not elegant, to be sure, but quick.

André Nicolas
  • 507,029
  • In OP's diagram, simply connect the (non-origin) end of the red segment to the right end of the horizontal radius of the big circle; this creates a right triangle with legs $\cos\phi$ and $\sin\phi$, hence area $\frac{1}{2}\cos\phi\sin\phi$ on the other hand, the altitude from the right corner to the hypotenuse (the blue vertical segment in OP's second diagram) is $\frac{1}{2}\sin 2\phi$, while the hypotenuse-base is $1$, so that the triangle's area is can also be computed as $\frac{1}{2}\cdot 1 \cdot\frac{1}{2}\sin 2\phi$. – Blue Mar 23 '13 at 03:21
2

If we are allowed to assume $$\sin(A+B)=\sin A\cos B+\cos A\sin B,$$

Put $A=B=x$

Alternatively , if we are allowed to use Euler Identity $e^{ix}=\cos x+i\sin x$

$e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x$

So, $$\sin x=\frac{e^{ix}-e^{-ix}}{2i}, \cos x=\frac{e^{ix}+e^{-ix}}2$$

and $$\sin2x=\frac{e^{2ix}-e^{-2ix}}{2i}$$

lab bhattacharjee
  • 274,582
1

A purely geometric proof can be done like this:

Construct triangle $\triangle$ABC such that it is a right angle at B and angle $\theta$ at A. Construct similar triangle $\triangle$BCD so that B is again the right angle and D is angle $\theta$. Finally, construct triangle $\triangle$ADE by extending AC such that the angle at E is a right angle.

Let AC = CD = 1. From triangle $\triangle$CDE, you can determine that DE = $\sin 2\theta$. From triangles $\triangle$ABC and $\triangle$BCD, you can determine that AB=BD=$\cos \theta$, so that AD=$2\cos\theta$. From triangle $\triangle$ADE, DE = $2 \cos\theta \sin\theta$. Therefore, $\sin 2\theta = 2\cos \theta \sin \theta$.

Glen O
  • 12,425
1

Let $ABC$ be any triangle with $<A=x$. Let $O$ be the center of the circumcircle. Then combining sin and cos law, you get the formula for $\cos(2x)$.

Then $BOC=2x$.

The cos Law yields

$$BC^2=BO^2+OC^2-2BO CO \cos(2x) \,.$$

By Sin law we have $BC= 2R \sin (x)$. Combining this with $BO=CO=R$, we get

$$4 \sin^2(x)=2-2 \cos(2x)$$

Now, you can get the desired formula from $\sin(2x)$ from $\sin^2(2x)+\cos^2(2x)=1$.

N. S.
  • 132,525
0

You can derive this formula also from a rhombus with all sides equal to, say 1. The acute angle is 2x and when you draw a diagonal you get two equal angles, x Drawing the other diagonal gives you a bunch of right triangles. Your double angle formula sin2x as well as the halfangle formula tan(x/2) can be easily derived from it. Do you see how to do tan(x/2)? There are two of them in terms of sinx and cosx. You need to think ourside the rhombus and draw a perpendicular to create another right triangle. Try it out...

imranfat
  • 10,029