A student I tutor asked me this question. The L'Hopital's approach is quick and easy, but is there a direct but rigorous way to show this without invoking L'Hopital's?
Asked
Active
Viewed 72 times
0
-
7You cannot use L'H since the derivative requires knowing the limit. – Andrew Chin Oct 02 '19 at 23:06
-
The typical proof is geometric and uses the squeeze theorem. – Andrew Chin Oct 02 '19 at 23:06
-
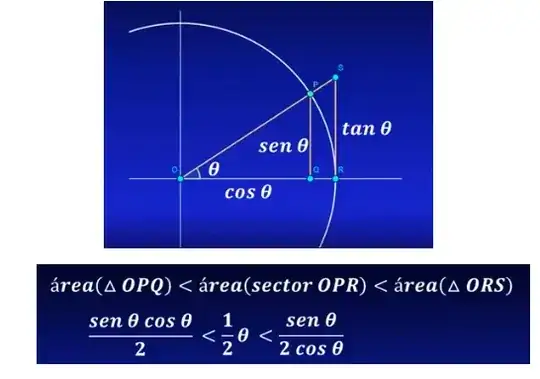
An elementary and acceptable proof is considering a point P on the unit circle in the first quadrant, along with it a triangle inside and outside the circle. Considering areas as P moves to the x axis results in the limit. I am sure this can be found somewhere on MSE. I am glad though you see that Hospital is not the way to go. – imranfat Oct 02 '19 at 23:09
-
See https://www.cut-the-knot.org/arithmetic/algebra/ElementaryLimit.shtml and https://math.stackexchange.com/questions/75130/how-to-prove-that-lim-limits-x-to0-frac-sin-xx-1 – Ethan Bolker Oct 02 '19 at 23:10
-
Take a look to any calculus book or in frequent question here at MSE. – user Oct 02 '19 at 23:11
-
I really like this proof on KhanAcademy: https://www.youtube.com/watch?v=5xitzTutKqM It isn't as rigorous as other proofs but it's very intuitive. Very easy to explain to a student. – Hossmeister Oct 02 '19 at 23:12
-
@hossmeister. What proofs are out there that dont use derivative of sine whatsover, only elementary properties? – imranfat Oct 02 '19 at 23:41