0

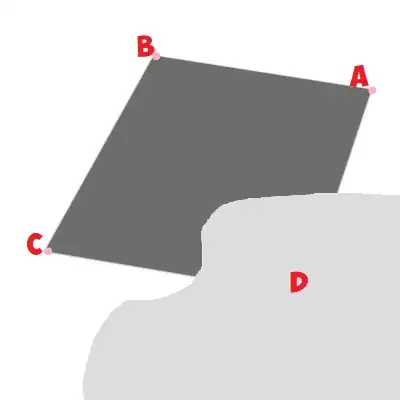
I have a picture of three vertices of a square of edge of length 1, that has one vertex covered.

Is it possible to recover the 2d coordinates (in the picture) of the 4th vertex?

Or is it not enough information?

For now I came up with a system of 18 equations for 19 variables:

let $ A,B,C,D $ denote 2D coordinates of the square (in the picture)

let $ a,b,c,d $ denote 3D coordinates of the squre (in reality)

assume the camera is at 0

and picture plane is at $z=\omega$

since $0, A, a$ are on a line (and similarily $0,B,b$; $0,C,c$; $0,D;d$)

$a_x = \alpha A_x$ $a_y = \alpha A_y$ $a_z = \alpha \omega$ $b_x = \beta B_x$ $b_y = \beta B_y$ $b_z = \beta \omega$ $c_x = \gamma C_x$ $c_y = \gamma C_y$ $c_z = \gamma \omega$ $d_x = \delta D_x$ $d_y = \delta D_y$ $d_z = \delta \omega$

since it is a square of side of 1, we also have:

$|a-b| = 1$

$|a-c| = \sqrt 2$

$|a-d| = 1$

$|b-c| = 1$

$|b-d| = \sqrt 2$

$|c-d| = 1$

visible vertices A,B,C; supposed square in gray

visible vertices A,B,C; supposed square in dark gray

Golob
  • 1,100
  • 1
    Using just the coordinates of the points $A,B,C$ you can't do it. But if you use the lines, it is easy: just extend the two incomplete sides to meet at $D$. – almagest Sep 27 '19 at 19:32
  • @almagest True, using the lines is easy. Could you prove that it is impossible? Either general proof or counter example? – Golob Sep 27 '19 at 19:52
  • 1
    Given two convex quadrilaterals, you can always find a projective transformation that maps one to the other. In particular, this means that the images of three points aren’t enough to determine the map uniquely. To put it more simply, $D$ can be almost anywhere. – amd Sep 28 '19 at 06:27

1 Answers1

0

See my answer to another question for how for points and their images define a projective transformation as long as no three are collinear. In your case that means that knowing just the corners is not enough information, since you could pick the fourth corner pretty much arbitrarily and still find a projective transformation.

On the other hand, in your example picture you have all four edges. Reconstructing the fourth corner as intersection of the corresponding edges would be easy.

MvG
  • 42,596