$R_f \cong R[x]/(fx-1)$

Question

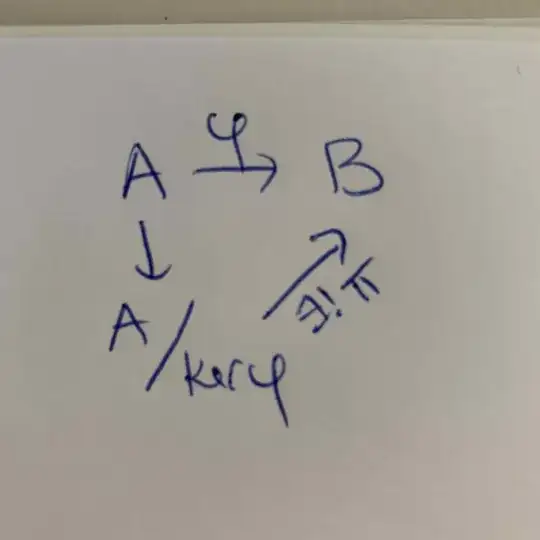
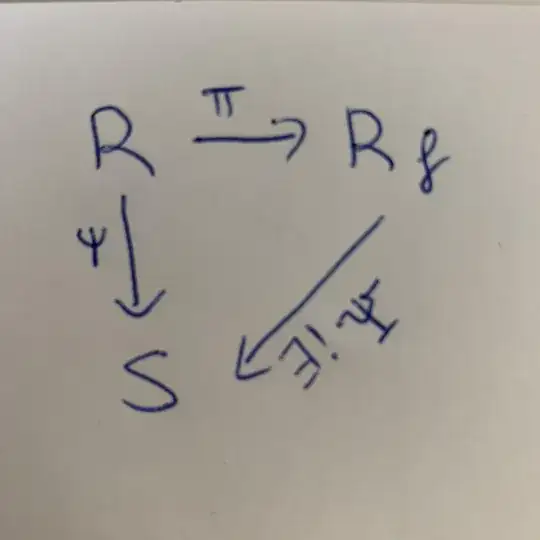Let $R$ be commutative ring with $1$. Let $f \in R$. Suppose $f$ is not nilpotent in $R$. We need to show $R_f \cong R[x]/(fx-1)$, with $D = \{f^n: n \ge 0\}$ and where $R_f = D^{-1}R$. I am given the following hint: [Show that the map $\phi : R[x] \to R_f$ gives a surjective ring homomorphism and the universal property in Theorem 36 gives an inverse.]

Theorem 36: Let $R$ be a commutative ring with 1 and let $D$ be a multiplicatively closed subset of R containing 1. Then there is a commutative ring $D^{-1}R$ and a ring homomorphism $\pi: R \to D^{-1}R$ satisfying the following universal property: for any homomorphism $\psi : R \to S$ of commutative rings that sends 1 to 1 such that $\psi(d)$ is a unit in $S$ for every $d \in D$, there is a unique homomorphism $\Psi: D^{-1}R \to S$ such that $\Psi \circ\pi = \psi$.

I'm not sure where to go after I define $\phi$. How does the theorem give me an inverse, and how does that show that the two rings are isomorphic? Help would highly, highly be appreciated.

Answer 1

I personally find it easier to draw diagrams for something like Thm. 36, which states the following:

here $S$ can be any ring, for example $R[x]/I$ with $I = ⟨−1⟩$. To apply theorem 36 you need construct such a $\psi: R \rightarrow R[x]/I$, so that

:→R[x]/I is a homomorphism of commutative rings that sends 1 to 1 such that () is a unit in R[x]/I for every ∈

as you already mentioned. You could probably construct $\psi$ through composition $\pi \circ i$ of following two homomorphisms: an embedding of $R$ in $R[x]$, $i: R \rightarrow R[x]$, $i(a) = a$ and a canocial projection of polynomials onto its equivalence classes wrt $I$, $\pi: R[x] \rightarrow R[x]/I$, $f \mapsto \overline{f} $.

The other homomorphism you apparently get by using a "standard" universal property of rings, which yields an isomorphism, if $\phi$ is surjective:

here you have $A = R[x]$, $B = R_f$ hence $\phi$, that you constructed should probably have $\ker(\phi) = ⟨−1⟩$.

TL;DR: Try to check if homomorphisms that you constructed have desired properties and if so, apply appropriate theorems

Answer 2

Here you take $S={\Bbb R}[x]/I$ with $I\langle fx-1\rangle$. Then $f^n+I$ is a unit in $S$, since in $S$ we have $f\cdot x=1$ and so $f$ is invertible and so is each power of $f$. Now apply the universal property above and you will get the result!