3

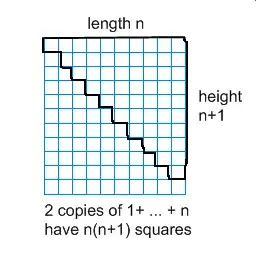
We know that Gauss has shown that the sum $S$ of the first $n$ natural numbers is given by the relation:

$$S=\frac{n(n+1)}{2} \tag{*}$$ The proof that I remember most frequently is as follows:

Let be $S=1+2+\dotsb+(n-1)+n \tag{1}$ We can write $S$ it also as: $\tag{2} S=n+(n-1)+\dotsb+2+1.$ By adding up member to member we get: $\tag{3} 2S=\underbrace{(n+1)+(n+1)+\dotsb+2+1}_{n-\mathrm{times}}.$ Hence we obtain the $(^\ast)$.

How many other simple methods exist to calculate the sum of the first natural numbers?

Sebastiano
  • 7,649

5 Answers5

3

Here is a proof using ideas from probability theory. Let $X$ be a random variable that is uniformly distributed on the set $\{1,\dotsc, n\}$. Then it is easy to see that $n+1-X$ has the same distribution as $X$ whence $$ E(n+1-X)=EX $$ i.e. $n+1-EX=EX$ so $$ EX=\frac{n+1}{2}\tag{0}. $$ But on the other hand, $$ EX=\sum_{k=1}^n kP(X=k)=\frac{1}{n}\sum_{k=1}^n k.\tag{1} $$ Combining $(0)$ and $(1)$ we get that $$ \sum_{k=1}^nk=\frac{n(n+1)}{2}. $$

Sri-Amirthan Theivendran
  • 31,116
2

The identity

$$\sum_{k=1}^{n}k=\frac{n(n+1)}{2}$$

is a classical result which can be easily proved by the following

enter image description here

user
  • 154,566
2

The expression of $S_n$ must be a quadratic polynomial (because the difference $S_n-S_{n-1}=n$ is a linear polynomial). As $S_0=0$, it is of the form $an^2+bn.$

By identification,

$$\begin{cases}S_1=a+b=1,\\S_2=4a+2b=3\end{cases}$$

and $$a=b=\dfrac12.$$

The Lagrangian polynomial by $(0,0)$, $(1,1)$, $(2,3)$ is $\dfrac{x^2}2+\dfrac x2$.

$$S(n)-S(n-1)=an^2+bn-a(n-1)^2-b(n-1)=a(2n-1)+b=n$$

so that

$$a=b=\dfrac12.$$

A posteriori:

$$S_n-S_{n-1}=\frac{n(n+1)}2-\frac{(n-1)n}2=n.$$

As an arithmetic progression is linear, the average term is the average of the extreme terms.

$$\frac{S_n}n=\frac{1+n}2$$ and $$S_n=\frac{n(n+1)}2.$$

Let the function defined by a geometric series

$$f(x):=\sum_{k=0}^n x^k=\frac{x^{n+1}-1}{x-1}.$$

We differentiate on $x$,

$$f'(x)=\sum_{k=0}^n k x^{k-1}=\frac{x^{n+1}-1}{x-1}=\frac{(n+1)x^n(x-1)-(x^{n+1}-1)}{(x-1)^2}.$$

Then with $x=1$, using L'Hospital,

$$f'(1)=\sum_{k=0}^n k =\lim_{x\to0}\frac{nx^{n+1}-(n+1)x^n+1}{(x-1)^2} =\lim_{x\to0}\frac{n(n+1)x^{n}-(n+1)nx^{n-1}}{2(x-1)}=\frac{n(n+1)}2.$$

  • Thank you very much also to you. Have you used the telescopic rule? :o) – Sebastiano Sep 26 '19 at 21:37
  • 1
    @Sebastiano The telescoping can be discussed in terms of binomial coefficients, viz.$$\sum_{k=1}^nk=\sum_{k=1}^n\binom{k}{1}=\binom{n+1}{2}$$by the hockey-stick identity. But we can also derive that without telescoping by a double-counting argument. – J.G. Sep 26 '19 at 21:42
  • @J.G. Very difficult for my students to understand. However thank you for your precious comment. – Sebastiano Sep 26 '19 at 21:45
  • 1
    @Sebastiano The double-counting argument I mentioned might be the easiest way for them to understand it. – J.G. Sep 26 '19 at 21:48
2

Certainly overkill, but we can do this with the method of generating functions: let $$f(x)=\sum_{k=0}^nx^n=\frac{1-x^{n+1}}{1-x}$$ So that $f'(1)=\sum_{k=0}^nk$. We just need to find $f'(x)$, and we proceed as usual: $$\frac{d}{dx}\frac{1-x^{n+1}}{1-x}=\frac{-(n+1)x^n(1-x)+(1-x^{n+1})}{(1-x)^2}$$ Taking the limit as $x\to1$, we have by L'hopital's rule and after simplification, $$\lim_{x\to1}\frac{-n(n+1)x^{n-1}(1-x)}{-2(1-x)}=\lim_{x\to1}\frac{n(n+1)}{2}=\frac{n(n+1)}{2}$$ From which we obtain the conclusion.

YiFan Tey
  • 17,431
  • 4
  • 28
  • 66
  • If you’re going with generating functions, why not instead compute $x^{n-1}^{-3}$? That only requires using the Generalized Binomial Theorem. – amd Sep 28 '19 at 07:29
  • @amd I never said you couldn't do that, of course. That would be another way. – YiFan Tey Sep 28 '19 at 07:33
1

Use can use the sum of AP to arrive at the same conclusion. $a=1, d=1$ $$S_n = {n\over 2}(2a+(n-1)d)$$ $$S_n = {n\over 2}(2+(n-1))$$ $$S_n = {n\over 2}(n+1)$$

Sam
  • 2,447