How to show that this graph is planar?
I am unable to write a formal proof
In the book the answer is given that this graph is planar. Can you kindly say how to prove that this graph has no subgraph homeomorphic to $K_5$ or $K_{3,3}$?
I find that this graph has two vertices $[0],[4]$ of degree $8$ and all other vertices are connected to these two.
How to show that this graph is planar?
Please help.
If you want to prove by showing it does not have a minor graph that is $K_5$ or $K_{3,3}$, you need only look at the degrees of the vertices. There are only two vertices with degree $3$ or more. If you delete edges/vertices or contract edges, you won't increase the number of such vertices. Both $K_5$ and $K_{3,3}$ have more vertices of degree $3$ or higher so cannot occur as a minor of this graph.
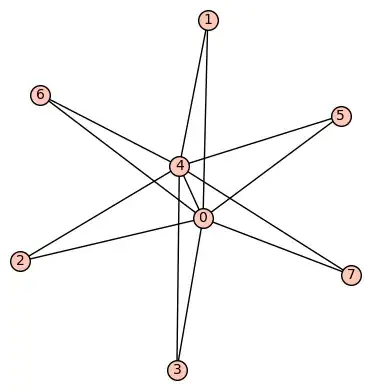
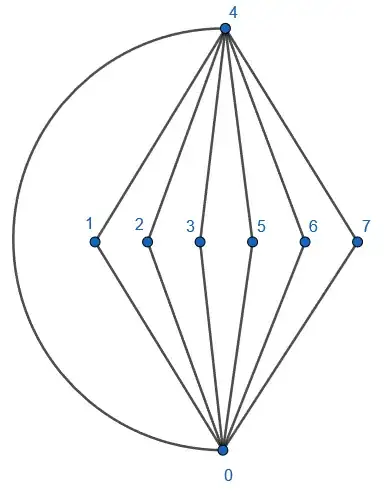
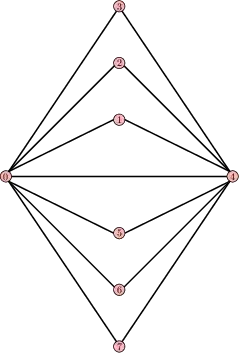
A graph is planar if there exist at least one drawing of this graph (called an embedding) on the plane with no crossing edges.
Therefore as explained by Bercy, you just need to show one drawing of this graph with no crossing edges. To do so take you vertex labelled 0, and pull it out of the other vertices, outside the star-like graph around the vertex 4. Remember that edges are not required to be straight line (even if there is some result proving that this is always possible). So you can use bent lines to join some vertices. You should be able to build such a planar drawing.
Edit I just noticed your other question here. There you were asked to prove that a graph is not planar. That's way you needed to prove that it includes $K_5$ or $K_{3,3}$ as a subgraph. Because otherwise you would need to exhibit all possible drawings. However, here to prove that a graph is planar, it is enough to exhibit one planar drawing.
Here is some specific drawing, that proves that graph could be embedded into the plane.
