2

Here is the problem I want to ask in my homework

The following Matlab script computes (1 − cos(x))/x2 in two ways:

format long
x = 1e−7;
y = (1−cos(x))/x^2;
cx = cos(x);
z = (1−cx)/acos(cx)^2; 
y
z

why is z much more accurate than y? Assume the floating number is 16 digits accurate.

The professor said that 1 - cos(x) will introduce great cancellation error with only 2 digits accuracy, however I am wondering why 1 - cx then will not be affected by the cancellation error? There seems to be not much difference.

Carl Christian
  • 12,583
  • 1
  • 14
  • 37
Yilin L.
  • 149
  • This underlying exercise is good because it emphasizes that not all representations of the same function are equally good. However, a word of caution is order. The suggested alternative breaks for $|x| \lesssim 10^{-8}$. Why? Below this threshold $r=\cos(x)$ rounds to $1$ and $s=\arccos(r)$ returns $0$. A better approach is to use a truncated Taylor series for small $x$. – Carl Christian Oct 14 '19 at 09:40

2 Answers2

1

This is kind of the same trick that you get when evaluating $\ln(1+x)$ as $\frac{\ln(1+x)x}{(1+x)-1}$.

The equivalent expressions $2\left(\frac{\sin(x/2)}{x}\right)^2=\frac1{1+\cos x}\left(\frac{\sin x}x\right)^2$ are evaluated exactly within the capabilities of the floating point format and thus can serve as the exact values $f_e(x)$. Comparing the two expressions $f_{\rm orig}(x)$ and $f_{\rm trick}(x)$ in question against these gives the plot

error plot

This confirmes the claimed difference in the floating point results.

Why does that happen? Clearly the floating point evaluation of $1-\cos(x)$ leads to catastrophic cancellation for $x\approx 0$, with $$ 1-\frac12x^2\le \cos x\le 1-\frac12x^2+\frac1{24}x^4. $$ The error will be of the scale $\delta=2^{-54}=5.55\cdot 10^{-17}$ independent of how small or large $x$ is. \begin{array}{ll} x&fl(1-fl(\cos x))-2\cdot fl(\sin(x/2))^2\\ \hline 0.0123 & -3.06558e{-}17\\ 0.00123 & -2.63537e{-}17\\ 0.000123& +3.59060e{-}17\\ 1.23e{-}05& +4.57838e{-}17\\ 1.23e{-}06& -5.50533e{-}17\\ 1.23e{-}07& -1.49834e{-}17\\ 1.23e{-}08& +3.53773e{-}17\\ 1.23e{-}09& -7.56450e{-}19\\ \end{array} where $fl(y)$ indicates floating point rounding of the argument. Then with $c_x=fl(\cos x)$ and $\bar x=fl(\arccos c_x)$ a value is computed that is in the center of the interval with $$ fl(\cos(u))=c_x\iff \cos(u)\in[c_x-\delta,c_x+\delta]. $$ With $\cos(u)-\cos(\bar x)=-2\sin(\frac{u-\bar x}2)\sin(\frac{u+\bar x}2)\approx -\bar x(u-\bar x)$ we get $|\bar x|\,|u-\bar x|\lesssim δ$.

The value $\frac{1-c_x}{\arccos(c_x)^2}=\frac{1-\cos\bar x}{\bar x^2}$ is now exact at the modified point $\bar x$, and the error is about $f'(\bar x)(x-\bar x)=\frac{\bar x}{12}(x-\bar x)\lesssim\fracδ{12}$ (using the derivative of $f(x)=\frac12-\frac1{24}x^2+\frac1{6!}x^4+...)$). This is below the relative precision at the result at $\approx \frac12$.

The observed error in the second formula to the reference formula is the floating point error of the remaining operations in $\frac{1-c_x}{\bar x^2}$.

Lutz Lehmann
  • 126,666
  • I think I almost understand the errors in two ways. However, there is a big issue I am so confused about. We get a large cancellation when doing 1 - cos(x), but when we assign u = cos(x) and do 1 - u, why there is no such big cancellation like the first one? – Yilin L. Sep 26 '19 at 01:56
  • When you compute $\arccos(c_x)$ you effectively compute $\arcsin(\sqrt{1-c_x^2})=\sqrt{1-c_x^2}(1+\frac16(1-c_x^2)+O((1-c_x^2)^2)$. This, or better its square essentially contains the same catastrophic cancellation error as was made in the numerator. Thus the errors cancel out. That is why I wrote that the value at $\bar x$ is computed exactly, in the whole interval of arguments with the same floating point cosine value, the arcus cosine picks the one where the floating point evaluation is the most exact and coincides with the other formulas. – Lutz Lehmann Sep 26 '19 at 03:44
1

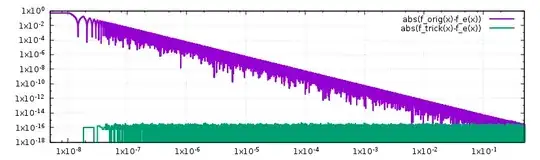
Let us define the two functions $$ \DeclareMathOperator{\fl}{fl} f(x) = \frac{1-\cos(x)}{x^2} \quad \text{and} \quad g(y) = \frac{1 - y}{\arccos(y)^2} \,. $$ We have that $$ f(x) = g(\cos(x)) \,. $$ When you evaluate $f(x)$ for $x = 10^{-7}$ catastrophic cancellation occurs for the following reason. The numerator is evaluated by computing $1 - \fl(\cos(x))$ (where $\fl$ denotes rounding to a floating point number). Since $\cos(10^{-7}) \approx 1$ many digits in the result cancel and error due to the digits that are lost, by rounding the value of $\cos(x)$, become significant. Thus, the overall result has a low accuracy.

At first sight, it looks like the same is true, if we first compute $y = \fl(\cos(x))$ and then computing $g(y)$. We are again subtracting two very similar numbers when evaluating $g$, hence cancellation should occur. This is, however, not the case.

First of all note that $g$ does not vary a lot at $y = 1$, because $$ \lim_{y \to 1} g'(y) = \tfrac{1}{12} \,. $$ Thus, if we perturb the input, the output will only change slightly, i.e., if $\bar{y} \approx y$ then $g(\bar{y}) \approx g(y)$.

Now, let $\bar{y} := \fl(\cos(x))$. The number $\bar{y}$ is (by definition) exactly represented by a floating point number. When a floating point computation unit subtracts two floating point numbers, it computes a result that is precise up to machine precision. Catastrophic cancellation occurs, when the numbers have to be rounded first.

To make this behavior clear, consider the following example. Assume we want to compute $$ 1.000 - 0.999 $$ using four digits of accuracy. It turns out, that three leading digits of the result are zero. To compute the remaining digits, the computer assumes, that the two numbers are given exactly by floating point numbers, i.e., all the remaining digits are zero. Thus we can compute $$ 1.000000 - 0.999000 = 0.001000 = 1.000 \cdot 10^{-3} \,. $$ In this case, the result is even exact.

However, if we instead intended to compute $$ 1.000431 - 0.999001 = 1.430 \cdot 10^{-3} \,, $$ in four digits accuracy the computer would have done the same thing and the values that the computer would produce would be very inaccurate.

Thus, by first computing a floating point representation $\bar{y} \approx \cos(x)$ and then computing $g(\bar{y})$ we feed the computation algorithm with a number that is exactly represented by a floating point value. Hence, the subtraction is precise up to machine precision. The only significant error that we are making is the error that results from computing $g(\bar{y})$ instead of $g(y)$.

H. Rittich
  • 631
  • In the second case how can you get 1 - x approximate 0.999999999 when x here is cos(1e-7)? Shouldn’t the result also be close to 0? – Yilin L. Sep 26 '19 at 12:24
  • @YilinLi My explanation was wrong. I have corrected the explanation, which should make more sense, now. – H. Rittich Sep 26 '19 at 14:10
  • Nice, that’s exactly what professor explained. But just a quick question, y = fl(cos(x)) is stored as a floating point in computer and thus the computation is very accurate, however, does this mean x = 1e-7 is not stored as a floating point? Because otherwise f(x) be precise because of floating point arithmetic. What type is x then? – Yilin L. Sep 26 '19 at 14:57
  • @YilinLi $x = 10^{-7}$ can be stored as a floating point number. And that is the reason, why $\cos(x)$ will be computed up to machine precision. However, $\cos(x)$ cannot. The result of $\cos(x)$ will be rounded and is then used in a subtraction. The whole point is not that the input was precise at some point. The point is that the rounding has to happen at the right place. – H. Rittich Sep 26 '19 at 15:03
  • @YilinLi To be more precise. The difference between $f$ and $g$ is that $g$ can be evaluated precisely in the case the $y$ is a floating point number. The function $f$, however, cannot. – H. Rittich Sep 26 '19 at 15:17
  • Thank you a lot, I think I got this. The reason why f is not accurate is that when we do 1 - cos(x), the intermediate value cos(x) is not stored and thus the computer just round by cutting the digits, which leads to catastrophic cancellation. But if we store cos(x) as a floating point y in computer first, then all the computation based on y is accurate because of the mechanics of floating point arithmetic. Is my understanding correct? – Yilin L. Sep 26 '19 at 15:37
  • @YilinLi Yes. The intermediate value $\cos(x)$ cannot be stored as a whole and needs to be rounded. If you round first, then all computations directly involving $y$ are conducted with high precision. This procedure, however, only works, because $g$ as a whole is not sensitive to slight changes in the input. – H. Rittich Sep 26 '19 at 15:46
  • @CarlChristian You are right. Thank you for noticing. I have corrected that mistake. – H. Rittich Sep 27 '19 at 08:38
  • You are very welcome. I am delighted to add this example to my collection. – Carl Christian Sep 27 '19 at 16:32