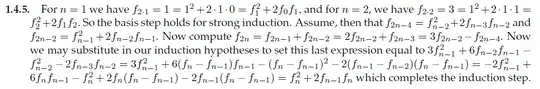Show $f_n^2+2f_{n-1}f_n = f_{2n}$

Question

The solution is above, but it seems like you have to know intuitively beforehand to calculate $f_{n-4}^2$ and $f_{2n-2}$. Is there a general methodology to prove these?

Answer 1

My favorite Fibonacci technique is the matrix formulation, which is well worth knowing and easily proved: $$ A^n= \begin{pmatrix}1&1\\1&0\end{pmatrix}^n= \begin{pmatrix}f_{n+1}&f_n\\f_n&f_{n-1}\end{pmatrix} $$

The identity $f_n^2+2f_{n-1}f_n = f_{2n}$ follows at once by looking at the $(1,2)$ entry of $A^{2n}=(A^n)^2$: $$ f_{2n} = (f_{n+1}+f_{n-1})f_n = (f_{n}+f_{n-1}+f_{n-1})f_n = (f_{n}+2f_{n-1})f_n $$

The matrix formulation typically removes the mystery of algebraic manipulations in induction proofs.

Answer 2

Equivalent to the matrix formula, one can use $\varphi^n=f_n\varphi+f_{n-1}$ where $\varphi^2=\varphi+1$ is the golden ratio (or anything satisfying some form of that equation) as shown in this question. From this the identity boils down to some simple algebra:

\begin{align}\color{blue}{f_{2n}}\varphi+\color{green}{f_{2n-1}}&=\varphi^{2n}\\&=(\varphi^n)^2\\&=(f_n\varphi+f_{n-1})^2\\&=f_n^2\varphi^2+2f_nf_{n-1}\varphi+f_{n-1}^2\\&=\color{blue}{f_n(f_n+2f_{n-1})}\varphi+\color{green}{f_n^2+f_{n-1}^2}\end{align}