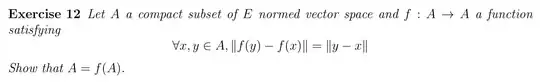Good morning, I'm trying to solve this problem:
My attempt:
Assume the contrary that there is $z \in A - f(A)$. Because, $f$ is Lipschitz continuous and $A$ is compact, $f(A)$ is compact. As such, $A-f(A)$ is open and thus there is $\mathbb B(z,r) \cap f(A) = \emptyset$.
After that, I'm stuck and unable to proceed. Could you please shed me some light? Thank you so much!