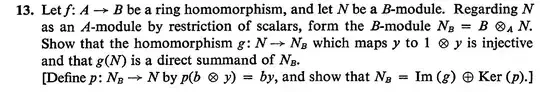This question is from the book Atiyah Macdonald- Commutative algebra.
Firstly I know that $g$ is an $A$-module homomorphism and $p$ is both an $A$-module and $B$-module homomorphism. Also $pg = id_N$. Now for any $b \otimes_A n \in N_B$,
$gp(b \otimes_A n) - b \otimes_A n$ $\in Ker(p) $
So, $b \otimes_A n = (gp(b \otimes_A n)-b \otimes_A n)+(b \otimes_A n+b \otimes_A n-gp(b \otimes_A n))$
So, I am left to show that $b \otimes_A n \in Im(g)$.
$b \otimes_A n = b(1 \otimes_A n)$ [ since $N_B$ is a $B$-module] $= b g(n) $
But I cannot show this is equal to $g(bn)$. How do I proceed?