2

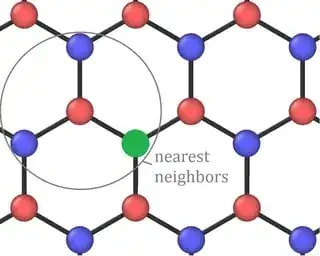
Imagine the periodic 2D arrangement of balls in the below figure. The red balls are fixed in the indicated positions, while all other sites have a probability $p$ of having a green ball, and a probability of $1-p$ of containing a blue ball. Let's also assume that the color of the balls for any two positions are statistically independent.

Now define the random variable $X_k$ as the total fraction of red balls that have $k \in \{0,1,2,3\}$ green balls as nearest neighbors. What is the probability distribution of $X_k$ for an arbitrary $k$?

                                                      enter image description here

My own thought: So I can easily calculate the probability of a specific red ball having $k$ green balls as nearest neighbors. It simply follows a binomial distribution:

$$\mathbb P (k\text{ green balls as nearest neighbors of a specific red ball})={3 \choose k} p^k (1-p)^{3-k}$$

But I don't know whether this is useful in my main question or not.

Edit: Just to clarify, the "lattice" in the above figure is periodic, so it extends to infinity in all directions. The red balls have deterministic locations with the indicated pattern, while the other sites can randomly be either blue or green.

Sahand Tabatabaei
  • 149
  • are you interested in the limit where the number of red balls $\to \infty$? if so, i would think $X_k \to {3 \choose k} p^k (1-p)^{3-k}$ with probability $1$ even though the red balls are not independent. OTOH if you are interested in the $9$ red balls shown in the diagram, that is a more tedious problem. – antkam Sep 15 '19 at 03:48
  • @antkam The "lattice" shown in the question is supposed to extend to infinity in all directions; so yes, the number of balls is infinite, and we want to know the probability distribution of the fraction of red balls that have a specific number of green balls as nearest neighbors. – Sahand Tabatabaei Sep 15 '19 at 03:52
  • And I don't exactly see why $X_k$ would have a binomial distribution. Could you elaborate on that please? The red balls are not random btw, they're fixed, It's the other sites in the lattice that either have blue, or green balls. – Sahand Tabatabaei Sep 15 '19 at 03:55
  • is my answer below helpful? do you have further questions? if not, pls accept my answer so this is marked as done. thanks! – antkam Sep 17 '19 at 02:10

1 Answers1

0

Consider some large number of balls, $N$, and index the balls by $j=1,2, \dots, N$. Also consider some fixed $k \in \{0, 1, 2, 3\}$.

Define the indicator random variable $I_{k,j}$ to be $1$ if ball $j$ has $k$ green neighbors, and $0$ otherwise. Note that $E[I_{k,j}] = {3 \choose k} p^k (1-p)^{3-k}.$ We now have:

$$X_k = \frac{S}{N} \,\,\,\,\,\,\,\,\text{where}\,\,\,\,\,\,\, S=\sum_{j=1}^N I_{k,j}.$$

You are correct that since $I_{k,j}$ are dependent, the sum $S$ is not Bernoulli. However, the dependence is so limited that the laws of large numbers still apply. In this example, you can partitioning the red balls into a small finite number of subsets s.t. no two red balls in the same subset are dependent.

One way to do the partitioning: First, notice that each red ball is dependent with only its $6$ nearest red neighbors. So do this: for every "odd-numbered" row of reds, color them alternately with $2$ different shades of red, and for every "even-numbered" row, color those red balls alternately with yet another $2$ different shades of red. Then with a total of $4$ different shades you have colored the reds s.t. two red balls sharing a blue/green neighbor have different shades of red. You have also broken up:

$$S=S_1 + S_2 + S_3 + S_4$$

where each $S_i$ represents the sum of $I_{k,j}$ in subset $i$ (that particular shade of red). Now it becomes true that each $S_i$ is a sum of i.i.d. variables and so $S_i/(N/4) \to E[I_{k,j}].$ When you sum them back up, you also get $X_k \to E[I_{k,j}]$.

BTW $S_i$ is now Bernoulli, but that fact is not really necessary. All we need is that $S_i$ is a sum of i.i.d. variables and the laws of large numbers apply.

Basically the laws of large numbers apply to cases where the variables being summed are dependent only to a small extent. The above is one example, but you can find more in the following, which I found after a few minutes of googling, and you may like these proofs or insights better.

Weak Law of Large Numbers for Dependent Random Variables with Bounded Covariance

https://mathoverflow.net/questions/2409/strong-law-of-large-numbers-for-weakly-dependent-random-variables

antkam
  • 15,363