5

A lot of calculators actually agree with me saying that it is defined and the result equals 1, which makes sense to me because:

$$ (-1)^{2.16} = (-1)^2 \cdot (-1)^{0.16} = (-1)^2\cdot\sqrt[100]{(-1)^{16}}\\ = (-1)^2 \cdot \sqrt[100]{1} = (-1)^2 \cdot 1 = 1$$

However, there are certain calculators (WolframAlpha among them) which contest this answer, and instead claim it is equal to:

enter image description here

Graphing this as an exponential function was not possible.

What's going on?

daedsidog
  • 997
  • 2
    Careful! – J.G. Sep 14 '19 at 18:51
  • 1
    Wolfram is taking the root before raising it to the 16th power. The principle 100th root of $-1$ has an angle of $180^o/100 = 1.8^o$. Then sixteen of these angles angles added together gives you $28.8^o$ – David P Sep 14 '19 at 18:52
  • 1
    For most people (who know about the nuances involved), the meaning of $(-1)^{2.16}$ depends on whether $2.16$ is interpreted as a real number or as a specific fraction (presumably $\frac{54}{25},$ and not $\frac{216}{200}$ or $\frac{108}{50}).$ – Dave L. Renfro Sep 14 '19 at 18:54
  • 2
    How do you define a non-integer power of a negative number? For positive reals and rational powers there is a unique positive real root, and a real function can be defined. $0^0$ is notoriously problematic and you might want to think about negative powers of zero . Where the power is $\frac pq\gt 0$ and $q$ is odd, the function can be extended to the reals. – Mark Bennet Sep 14 '19 at 19:01
  • 2
    It's a matter of definition. If $q = \frac ab; a\in \mathbb Z; b\in \mathbb N; \gcd(a,b) = 1$ and if $k < 0$ then is it a valid definition to define $k^q $ as $\sqrt[b]{k^a}$? It can be argued that is valid if $a$ is even but I'd say it has too many issues and handwaving and is inconsistant when we do bring in complex analysis to be acceptable. I'd say that definition holds if $k > 0$ but if $k < 0$ we will need to consider principal complex roots. By squaring $(-1)$ you are deliberating and artificially avoiding them. I'd say that is no good. – fleablood Sep 14 '19 at 19:01
  • tl;dr; I'd say that $(-1)^{0.16} = \sqrt[100]{(-1)^{16}}$ is not valid. I'd say for $x \not \in \mathbb Z$ that $b^x$ is not defined for $b < 0$ unless one uses the complex definition which would (brain farts obliging) evaluate to $|b|^xe^{\pi ix}$. – fleablood Sep 14 '19 at 19:12

4 Answers4

6

$(-1)^{2.16}=(-1)^{\frac{54}{25}}=\exp({\frac{54}{25}(2k+1)i\pi})=\exp({\frac{4}{25}(2k+1)i\pi})$

is a set of $25$ numbers corresponding to $k=0,...24$ as the exponential above has period $25$.

Choosing $k=12$ shows that $1$ is indeed in this set, though it doesn't correspond to the usual "principal" value which is for $k=0$ and which in this case, gives $\exp({\frac{4}{25}i\pi})$ and this is what Wolfram Alpha gave

Edit later - just to make it clear, here $\exp(z)=\sum{\frac{z^n}{n!}}$ is the uniquely defined usual entire exponential function

Conrad
  • 27,433
4

If we stay strictly in the real domain, then exponentiation is defined by the formula $x^y=\exp(y\ln(x))$.

Since the logarithm is defined only on positive numbers, exponentiation is also well defined only on positive bases $x$.

With this definition $(-1)^{2.16}$ is undefined.

However, since it also comes from rational exponentiation by continuity, which is merely an extension of integer exponentiation where things like $(-1)^n$ are perfectly defined, it is possible to extend exponentiation to negative real numbers as well, but with limitation to rational exponents.

If we call $\mathbb Q_{odd}=\{\frac pq\in\mathbb Q\mid p\in\mathbb Z, q\in\mathbb N^*, \gcd(p,q)=1\text{ AND } q\text{ odd}\}$

Then for $x<0$ we have $x^r$ defined for any $r\in\mathbb Q_{odd}$ by $$x^r=x^{\frac pq}=\sqrt[q]{x^p}=\left({\sqrt[q]{x}}\right)^p$$

Since the $q-$root is an odd function, it is perfectly defined for negative numbers.

Note that we explicitly require that $\gcd(p,q)=1$ to avoid contradictions like $-1=(-1)^{\frac 13}=(-1)^{\frac 26}=\sqrt[6]{(-1)^2}=1$

Considering this $(-1)^{2.16}=(-1)^{\frac {54}{25}}=1$ would be a reasonable answer.

Now it is also possible to take some high, and examine the situation on the complex domain.

$z_1^{z_2}=\exp(z_2\ln(z_1))$ is defined by the same formula that in the real case, but this time the logarithm has an extended definition.

The price to pay is that since $\exp$ is a $2i\pi-$periodic function, its inverse, the logarithm becomes multi-valued, meaning there will be more than one value per arithmetic expression.

We define $$\ln(z)=\ln|z|+i(\arg(z)+2k\pi)\quad k\in\mathbb Z$$


Let's examine the consequences for $(-1)^{2.16}$

$\ln(-1)=\underbrace{\ln(1)}_0+i(\underbrace{\arg(-1)}_{\pi\text{ from }e^{i\pi}=-1}+2k\pi)=(2k+1)i\pi$

Also since $2.16$ is in fact rational $\frac {54}{25}$ as we already seen, we won't get an infinite number of values for the expression, yet still $25$ different ones.

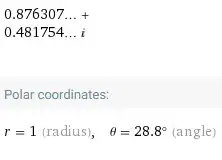
Let's call them for $k=0\cdots24$ $$z_{[k]}=\exp(\frac{54(2k+1)}{25}i\pi)=\exp(\frac{108k}{25}i\pi+\frac{54}{25}i\pi)=z_{[0]}\,\phi^k$$


With $\begin{cases}z_{[0]}=e^{(2.16i\pi)} & \text{is called the principal value at }k=0\\\phi=\exp(\frac{108}{25}i\pi) & \text{is a cyclic multiplicative factor (in this case a rotation)}\end{cases}$


As noted by Conrad, when $k=12$ then $z_{[12]}=1$ the answer found in the rational exponentiation case is effectively among the results, although it is not the principal value.

zwim
  • 28,563
2

I don't think you are allowed to split negative numbers up like that. Since $-1=e^{i\pi}$ then $$(-1)^{2.16}=e^{i\pi\cdot 2.16}$$ which is not a real number.

cmk
  • 12,303
Brandon O. Salazar
  • 21
2

The problem is that the exponential function: $$f:\mathbb{R}\rightarrow\mathbb{R}, f(x) = ab^x$$ is only defined for $b\in(0,\infty)$ and $a\neq0$ so $(-1)^x$ is not an exponential function, thus it doesn't have its proprieties.

On the other hand $(-1)^{2.16} = e^{2.16\log(-1)} = e^{2.16\pi i} = \cos(2.16\pi) + i \sin(2.16\pi)$ which gives the same value as WolframAlpha.

The graphing is not working because the function $(-1)^x = \cos(x\pi) + i \sin(x\pi)$ takes real values $\iff \sin(x\pi) = 0 \iff x\in\mathbb{Z}$.

LIR
  • 1,050
  • 6
  • 10