1

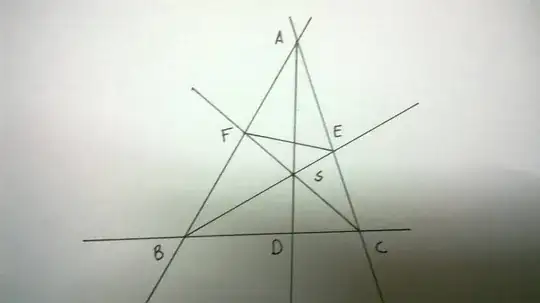
Consider this triangle. Suppose point <span class=$S$ tend towards Point $D$ along $AD$">

In the figure suppose the point $S$ tends to $D$ along Line $AD$ . According to Ceva $$ \frac{AF}{FB} \cdot\frac{BD}{DC}\cdot\frac{CE}{EA} =1$$ as we see if S tends to D $ \frac{AF}{FB} $ increases and $ \frac{CE}{EA} $ decreases And Ceva's theorem is valid and in the limiting case it seems to be valid, but is it valid when the point lies on the triangle, and what does the formula look like when the point is on the triangle?

J.G.
  • 115,835
Tamaghna Chaudhuri
  • 385

1 Answers1

2

It's not valid when $S=D$, because what that formula would then contain is a division by $0$, the length of $FB$. That's nonsensical. On the other hand, what would hold is $$ AF\cdot BD\cdot CE=FB\cdot DC\cdot EA $$ For any other case is exactly the same result, but it doesn't turn into garbage if $S$ lies on one of the sides of the triangle.

This result is, however, a bit more difficult to remember, and a bit more difficult to make some kind of direct geometric sense of. I suspect that this is why the variation with ratios is more prevalent.

Arthur
  • 199,419
  • The ratio form also helps keep straight how to assign signs. – Blue Sep 11 '19 at 15:33
  • @Blue True. That's part of what I meant by "remember". Although in my opinion sign is not a very essential part of the result. It's almost as good with all lengths assumed to be positive. Especially if one remembers in some other way that either none or exactly two of $D,E,F$ can be outside of the triangle. – Arthur Sep 11 '19 at 15:42
  • I should have written "especially helps" instead of "also helps". :) ... In any case, tracking signs becomes more of an issue when distinguishing Ceva from Menelaus, or when dealing with generalizations such as the Extended Ceva's Theorem in this answer. – Blue Sep 11 '19 at 16:51