Is there a name for an ellipsoid with an irregularly shaped cross-section?

Question

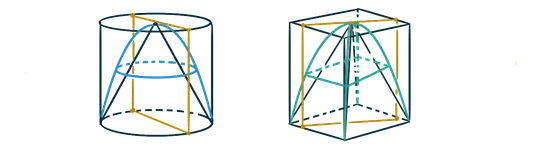
Start with a circular region in the plane, and build a right-circular cylinder of over it. Next construct the right-triangular cone with apex at the center of one of the bases of the cylinder, and between them construct the half-ellipsoid with a vertex at that same apex. I just learned a well-known fact that the ratios of the volumes of these three solids will be 1 : 2 : 3.

But let's instead start with a base of some other (convex?) shape. You can still build the cylinder over the base by crossing it with $[0,h]$ for some height $h$, and you can still build the cone over this by taking a point in the center of one of the bases of the cylinder as the apex of the cone, and constructing the locus of all lines connecting a point in the other base to that apex. But is there a canonical way to construct the analogue of the ellipsoid in this general situation? Here's an image of what I'm thinking in the case of a square-based cylinder and cone.

The only requirements I can think of for this generalized ellipsoid would be that it needs cross-sections all similar to the base, and it needs to have the correct ratio with the other two volumes, 1 : 2 : 3. And I suppose it should have some relation to the fact that a usual ellipse is the solution set to a quadratic polynomial. But I don't see an obvious (unique) way to do this. And it would be nice if this construction generalized to higher dimensions.

Answer 1

$\newcommand{\Reals}{\mathbf{R}}\DeclareMathOperator{\Vol}{vol}$This isn't strictly natural, but it does generalize the situations depicted and has flexibility that may allow the construction to be modified to suit.

Let $K$ be the closure of a bounded, non-empty open set in $\Reals^{n}$ (convex if desired). Let $O$ denote the origin of $\Reals^{n}$ (in $K$ if desired, but not necessarily). For each non-negative real $c$, let $cK$ be result of scaling $K$ by $c$ about the origin $O$; precisely, $$ cK = \{y \in \Reals^{n} : \text{$y = cx$ for some $x$ in $K$}\}. $$ The $n$-dimensional volume of $cK$ is $c^{n}\Vol{K}$.

Fix a positive height $h$, and for each positive exponent $r$ consider the solid of dimension $(n + 1)$ with base $K$ whose slice at height $z$ is $[(1 - z/h)^{r}K] \times \{z\}$. Geometrically, use an $r$th power function to scale $K$ to a point as the slice climbs to height $h$. By Cavalieri's principle, the volume of this solid is \begin{align*} \int_{0}^{h} \Vol[(1 - z/h)^{r}K]\, dz &= \Vol(K) \int_{0}^{h} [(1 - z/h)^{r}]^{n}\, dz \\ &= h\Vol(K) \int_{0}^{1} u^{rn}\, du \\ &= \tfrac{1}{rn+1} h\Vol(K). \end{align*} If $r = 0$ we have the cylinder $K \times [0, h]$ of volume $h\Vol(K)$. If $r = 1/2$, we have an analog of the paraboloid, of volume $\frac{1}{n/2+1} h\Vol(K)$. If $r = 1$ we have the cone, of volume $\frac{1}{n+1} h\Vol(K)$.

When $n = 2$ this reduces to $h\Vol(K)$, $\frac{1}{2} h\Vol(K)$, and $\frac{1}{3} h\Vol(K)$, giving volumes in arithmetic progression. Generally, picking values $r = k/n$ for $0 \leq k \leq n$, so that $rn + 1 = k + 1$, gives solids whose volumes are in harmonic progression: $h\Vol(K)$, $\frac{1}{2} h\Vol(K)$, $\frac{1}{3} h\Vol(K)$, ..., $\frac{1}{n+1} h\Vol(K)$.