5

I am having trouble understanding visually what a gradient is. My understanding is it is a generalisation of tangential slopes to higher dimensions and gives the direction of steepest ascent. There are 4 different pictures I have:

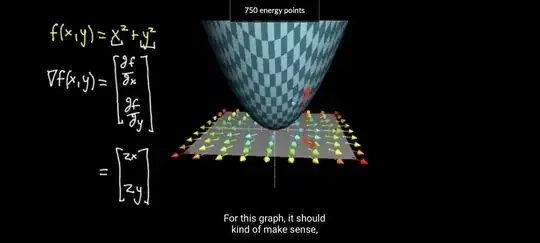
1) From Khan Academy. How does it make sense to have a 2d gradient when your function is 3d? And shouldn't it be tangential to the function? The only way this makes sense to me is if you consider it as the projection of the tangential gradient vector onto the x-y plane. Is this right?

Gradient acc to Khan academy

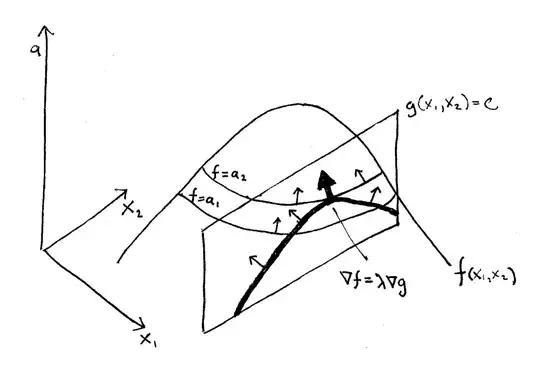
2) From a Medium article explaining Lagrange Multipliers. I understand the gradient for f but I'm not able to understand the gradient of g visually. It is a plane right?

Medium Article

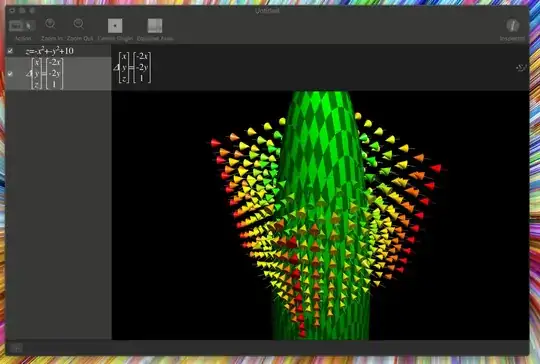
3) I have plotted some samples from MacOS Grapher. I'm assuming Vector Field Cartesian form is the Gradient Vector. Why are the arrows going inward? Shouldn't they be tangential to the curve?

MacOS Grapher

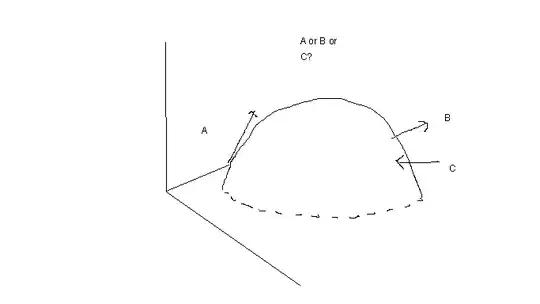
4) Finally, I have drawn some 3d curve. Could you tell me which gradient is correct? A, B or C?

A or B or C?

Any help appreciated. Sorry for the lengthy post but I have been breaking my head on this for a while. Thanks in advance.

Edit: Changed Legrande to Lagrange.

Nitin
  • 277
  • 1
    Related question (and I'm sure there are others). – Arthur Sep 05 '19 at 14:59
  • 2
    Imagine you're a mosquito flying around in $\mathbb R^3$, and the function $f$ tells you the temperature at each point $x \in \mathbb R^3$. You like warm weather. The gradient $\nabla f(x)$ is a vector in $\mathbb R^3$ that tells you which direction to move in (starting from the point $x$) so that the temperature increases as rapidly as possible. The magnitude of the gradient tells you how exactly how rapidly the temperature increases when you move in that special direction. – littleO Sep 06 '19 at 07:06

1 Answers1

6

  1. The function is two-dimensional, as in, it takes in two real numbers as input. The domain of the function is the plane, so the gradient also lives in the plane. Yes, the graph is drawn in 3-dimensional space, but that's because you need three dimensions to accurately represent two-dimensional input and one-dimensional output.

    If you instead visualise the function as simply a number for each point in the plane (it's boring, and not easy to draw, but in some sense truer to what's actually going on), then maybe this intuition works a little better. Yes, in your graph example, the gradient is sort of a projection of the steepest tangent vector at each point, but really, it's the other way around.

  2. It's Lagrange multipliers, not Legrande. And it's not so strange that you don't really understand the drawing, because I barely do. At least without an accompanying explanation. They seem to have drawn the graph of a function $f$ (as in 1.), and the constraint $g(x_1, x_2) = c$, but again, the arrows really should be in the $x_1x_2$-plane, not tangent to the graphs. And in the plane, $g(x_1, x_2) = c$ is a line, the gradient of $g$ is orthogonal to that line (see 4.), and when the gradient of $f$ is parallel to the gradient of $g$, then that means that moving along $g$ doesn't change the value of $f$, which again is a characteristic of extremal points. This is the main idea behind Lagrange multipliers.

  3. Again, you're mixing 2d and 3d. What you have is the graph of the function $z(x, y) = -x^2-y^2$. It's a function with a two-dimensional domain, and thus the gradient ought to live in the $xy$-plane. However, your vectors are in 3d. So what's going on there?

    Note that the $x$ and $y$ components of your vectors do corespond to the gradient of the function $z$, so if you take away the $z$-component from your vectors, they do indeed, at each point, point in the direction where the graph increases the most: straight in towards $(0,0)$.

    The same graph can also be seen as the level set $g(x, y, z) = 0$ for $g(x, y, z) = -x^2-y^2-z$. Taking the gradient of this function $g$, we get $[-2x, -2y, -1]$. Note that if you plot this vector field (change the sign of the $z$ component compared to your drawing), then the vectors are orthogonal to the surface (see 4.), and pointing inwards because that's the direction the surface moves if you increase the $0$ on the right-hand side of $g(x, y, z) = 0$.

  4. Is this the level surface of some function in three variables, or is it the graph of a function in two variables? If it is the graph of a function in two variables, I believe you already know my answer: A is the closest, but needs to be projected down into the $xy$-plane.

    On the other hand, if we have some function $f$ of three variables, and this graph is the level set $f(x, y, z) = c$ for some constant $c$, then B and C are actually gradients of $f$. They are, in a sense, both correct: if $f(x, y, z) = c$ gives the surface and $B$ is the gradient of $f$, then $-f(x, y, z) = -c$ gives the same surface, and $C$ is the gradient of $-f$. At least if you move it so that it starts at the graph.

    This is because the gradient points toward the direction of greatest increase of a function. And moving along a level set doesn't change the value of a function at all. So assuming differentiability, moving along the level set and moving in the direction of greatest increase must be orthogonal. So the gradient of $f$ is orthogonal to any of its level sets. The direction of the gradient tells you in which direction the level set will move if you increase the constant $c$, and the size of the gradient tells you how fast the surface will move at that point.

    Of course, a function like this $f$ will likely have gradients everywhere in space, not just on the level surface (just like functions that take two inputs have a gradient everywhere in the plane). These other gradients are orthogonal to other level sets.

Arthur
  • 199,419
  • Finally! Makes some sense to me. I'm going to have to reread your answer a few more times to unmuddle my head. But I think I got the gist of it. Thank you so much! This is the link to the Medium article: https://medium.com/@andrew.chamberlain/a-simple-explanation-of-why-lagrange-multipliers-works-253e2cdcbf74 – Nitin Sep 05 '19 at 15:18
  • 1
    @Nitin Take your time. This is the kind of stuff that takes time to get, but eventually, with practice, can become obvious and almost trivial. – Arthur Sep 05 '19 at 15:39