0

Self-studying “Basic Mathematics” by Serge Lang, got stuck doing final problem of chapter 5.

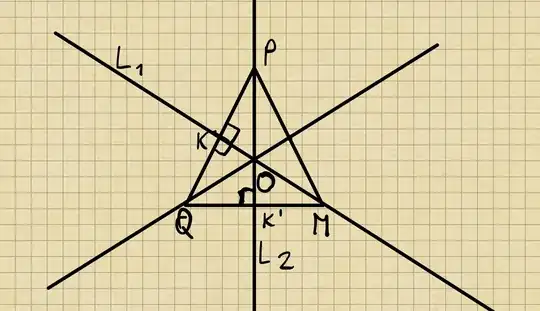
enter image description here

I took a sample triangle and labeled two lines and points.

enter image description here

As L1 is the perpendicular bisector of segment PQ, I know KP = KQ. Points K, Q and M form a right triangle.

That’s the information I gathered, do not know how to proceed from there. Any help would be appreciated.

Gerry Myerson
  • 179,216
F. Zer
  • 2,325
  • 1
  • 8
  • 21
  • 4
    I would caution you that you should draw a very general triangle $\triangle PQM$. Yours is isosceles and almost equilateral. Make it very generic, or else you'll be led to all sorts of false lines of reasoning. – Ted Shifrin Sep 04 '19 at 23:22
  • 2
    It's not just that KP=KQ for that specific point K. Any point X on L1 satisfies XP=XQ. So what can you say about the points on L2 and L3? And what can you say about the point where they meet? –  Sep 04 '19 at 23:24
  • Thank you @Ted Shifrin. How do I draw a generic triangle? – F. Zer Sep 04 '19 at 23:52
  • Will try to come up with an answer, @Matthew Daly. – F. Zer Sep 05 '19 at 00:17
  • 1
    @F.Zer A very philosophical question. Practically, when I want to make sure that I won't be misled, I try to draw a scalene triangle where none of the angles are right. In a sense that can be made precise, almost all triangles fit this description, so it's probably a good starting point. In general, a "generic" version of something is a version that has no unnecessary symmetry (like congruent sides) and no unnecessary "special" features (like a right angle). – Charles Hudgins Sep 05 '19 at 02:27
  • The lines shouldn't go through the vertices. That's very misleading as they don't in general. – fleablood Sep 05 '19 at 23:55
  • the way you drew it it looks like KO and OM are colinear. They almost certainly aren't. OM is not part of line 1. – fleablood Sep 05 '19 at 23:59

4 Answers4

1

Since $L_1$ is the perpendicular bisector of $\overline{PQ}$, it is also the line containing the altitude of $\triangle OPQ$ that passes through $O$ (since it is on $L_1$ as it is the intersection of $L_1$ and $L_2$). As such, $d(O,P)=d(O,Q)$ since they are the two equal sides of an isosceles triangle.

Apply the similar approach for $L_2$. Since $L_2$ is the perpendicular bisector of $\overline{QM}$, it is also the line containing the altitude of $\triangle OQM$ that passes through $O$. As such, $d(O,Q)=d(O,M)$.

The transitive property therefore tells us $d(O,P)=d(O,M)$.

Note: you may have to apply more algebra if you need a more rigourous explanation.

More info: $O$ in this case is also called the circumcentre (the center of the circumscribed circle for the triangle).

Andrew Chin
  • 7,389
  • Thank you. Could the explain the meaning of “altitude” of △ ? – F. Zer Sep 05 '19 at 11:08
  • The altitude of a triangle from a vertex is the straight-line distance from the vertex to the opposite side length. The altitude that passes through $O$ is the line segment that touches $O$ and meets $\overline{PQ}$ at a right angle. – Andrew Chin Sep 05 '19 at 14:40
  • Thanks for your answer. Did you meant “Since 2 is the perpendicular bisector of ” ? Also, how did you spot they were isosceles triangles? – F. Zer Sep 05 '19 at 23:10
  • 1
    You can try this for yourself: perpendicularly bisect a line segment $\overline{AB}$ using a line $L$, then pick any point $P$ on $L$. $ABP$ is an isosceles triangle since $d(A,P)=d(B,P)$. – Andrew Chin Sep 05 '19 at 23:13
  • Perfect. I see now that two sides are equal. – F. Zer Sep 06 '19 at 01:45
1

I'm going to offer a solution in the context of Lang's own presentation. This question is expecting one to use the Corollary to the Pythagoras Theorem that Lang provided on pg128. The proof of this corollary is on pg128 and exercise 9 from the same section.

Serge Lang Perpendicular Bisector

We know that:

  • if M lies on the perpendicular bisector PQ, then d(P,M) = d(Q,M). (Proven in ex9 using pythag.)

SO, since L1 is the perpendicular bisector of PQ, and O is on L1, d(P,O) = d(Q,O).

The same goes for L1 and having O on that line as well: since L2 is the perpendicular bisector of QM, and O is on L2, d(Q,O) = d(M,O).

We have: d(Q,O) = d(M,O) and d(P,O) = d(Q,O) from our assumptions of L1 and L2. Therefore, d(O,P) = d(O,M) from the transitive property. This relation ensures that O lies on the perpendicular bisector of PM because, as Lang proved on pg128:

  • Given two distinct points on the plane, P and Q, let M also be a point on the plane, d(P,M) = d(Q,M) if and only if M lies on the perpendicular bisector of PQ.

So, since we have d(O,P) = d(O,M), we know O must lie on the perpendicular bisector of PM.

Therefore, the perpendicular bisectors of the sides of the triangle PQM, defined by the set of segments PQ, QM, PM, meet in a point, in this case point O.

John Gardner
  • 11
0

We can see that $\triangle OKQ \cong \triangle OKP$ because $KQ=KP$, $KO$ is a common side and $\angle OKQ \cong \angle OKP$. Thus, $PO=OQ$. Apply the same reasoning to show that $OQ=OM$.

Vasili
  • 10,690
0

Use the definition of perpendicular bisector that the perpendicular bisector of $AB$ is all the points $X$ so that $AX = XB$. You don't need to find any congruent triangles.

Because $L_1$ is perp bisector of $PQ$ we have $OP = OQ$.

Because $L_2$ is perp bisector of $QM$ we have $OQ = OM$.

So $OP = OM$.

Therefore $O$ is a point on the perp bisector of $MP$.

That's all there is to it.

fleablood
  • 124,253